Question
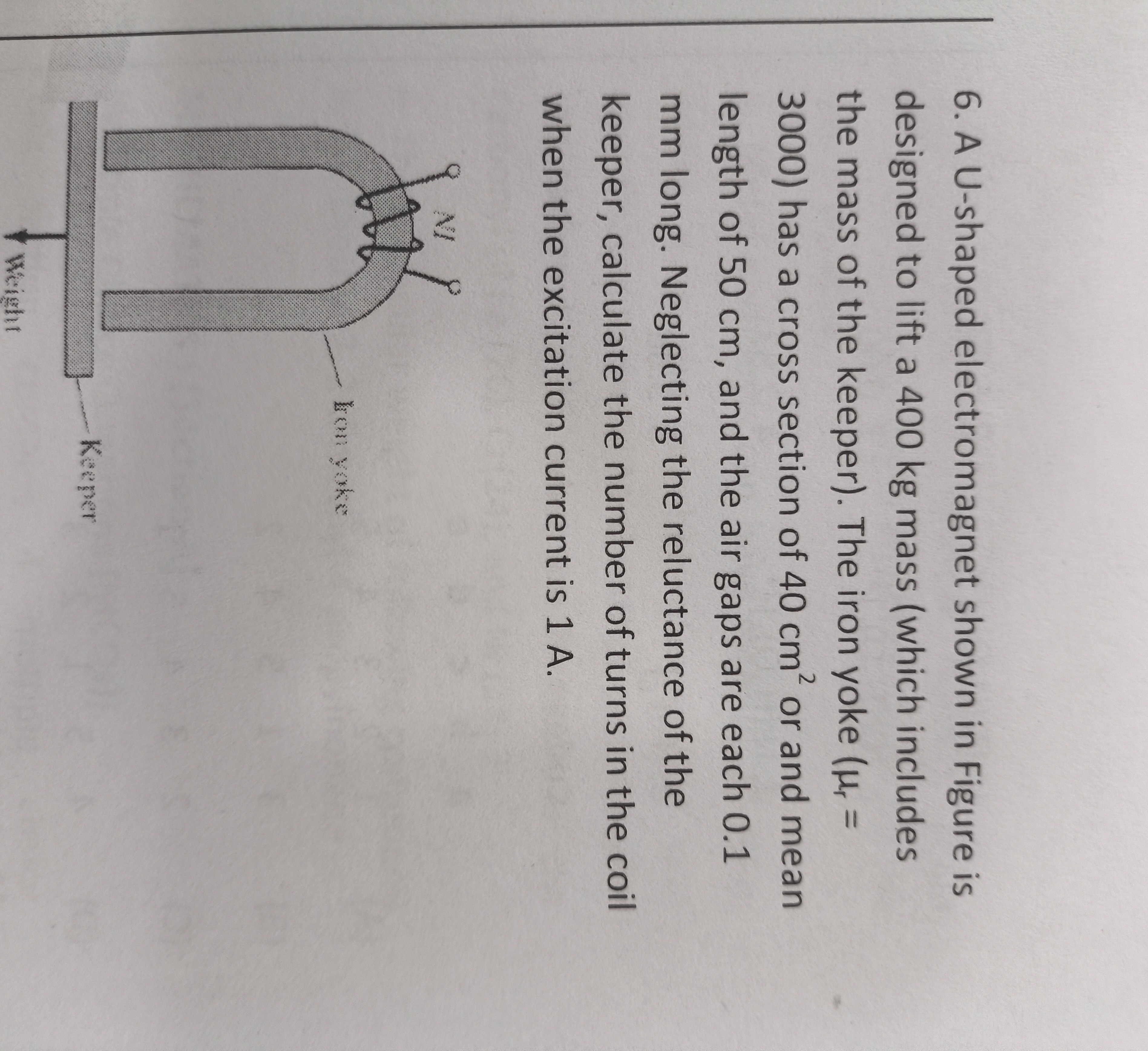
Question: A U-shaped electromagnet shown in Figure is designed to lift a 400 kg mass (which includes the mass ...
A U-shaped electromagnet shown in Figure is designed to lift a 400 kg mass (which includes the mass of the keeper). The iron yoke (μr = 3000) has a cross section of 40 cm2 or and mean length of 50 cm, and the air gaps are each 0.1 mm long. Neglecting the reluctance of the keeper, calculate the number of turns in the coil when the excitation current is 1 A.
324
Solution
To calculate the number of turns in the coil, we need to determine the required magnetic field strength (B) to lift the given mass and then use the magnetic circuit analogy (Ampere's Law) to find the necessary magnetomotive force (MMF), from which the number of turns can be derived.
1. Convert all given parameters to SI units:
- Mass to be lifted, M=400 kg
- Relative permeability of iron yoke, μr=3000
- Cross-sectional area of yoke, A=40 cm2=40×(10−2)2 m2=40×10−4 m2=4×10−3 m2
- Mean length of iron yoke, lm=50 cm=0.5 m
- Length of each air gap, lg=0.1 mm=0.1×10−3 m=1×10−4 m
- Excitation current, I=1 A
- Permeability of free space, μ0=4π×10−7 H/m
- Acceleration due to gravity, g=9.8 m/s2
2. Calculate the force required to lift the mass: The force required to lift the mass is equal to its weight. F=M×g F=400 kg×9.8 m/s2=3920 N
3. Relate the magnetic force to the magnetic field (B) in the air gap: The magnetic force exerted by an electromagnet on a ferromagnetic material (keeper) is given by F=2μ0B2A for one pole. Since the U-shaped electromagnet has two poles acting on the keeper, the total force is the sum of forces from both poles. Ftotal=2×2μ0B2A=μ0B2A We need to find the magnetic field B: B2=AFtotalμ0 B=AFtotalμ0 Substitute the values: B=4×10−3 m23920 N×4π×10−7 H/m B=3920×π×10−4 B=3.92×π×10−1 B=1.2315 (approximately, using π≈3.14159) B≈1.1097 T
4. Apply Ampere's Circuital Law (Magnetic Circuit Analogy) to find the number of turns (N): The total magnetomotive force (MMF), NI, is the sum of the MMF drops across the iron yoke and the two air gaps. NI=Hmlm+2Hglg Where Hm is the magnetic field intensity in the iron yoke and Hg is the magnetic field intensity in the air gap. We know that B=μH, so H=B/μ. For the iron yoke, μm=μrμ0, so Hm=μrμ0B. For the air gap, μg=μ0, so Hg=μ0B. Substitute these into the MMF equation: NI=μrμ0Blm+2μ0Blg Factor out B/μ0: NI=μ0B(μrlm+2lg) Now, substitute the known values: N×1 A=4π×10−7 H/m1.1097 T(30000.5 m+2×1×10−4 m) N=4π×10−71.1097(0.00016667+0.0002) N=12.566×10−71.1097(0.00036667) N=(8.830×105)×(3.6667×10−4) N≈323.7
Rounding to the nearest whole number, the number of turns N≈324.
