Question

A metal sphere of radius 1 m is charged with $10^{-2}$ C in air. Its bulk modulus is $\frac{10^{11}}{4\pi^2} \frac{N}{m^2}$

The volume strain in the sphere is

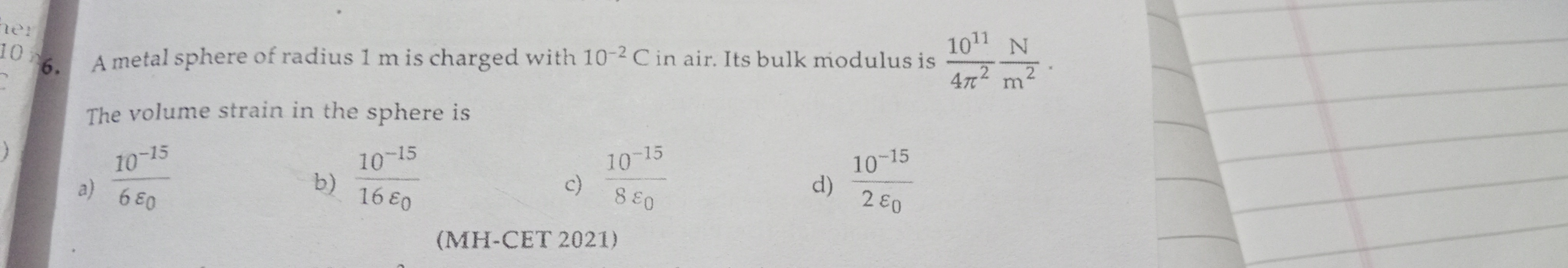
• A. $\frac{10^{-15}}{6\epsilon_0}$
• B. $\frac{10^{-15}}{16\epsilon_0}$
• C. $\frac{10^{-15}}{8\epsilon_0}$
• D. $\frac{10^{-15}}{2\epsilon_0}$

Answer 1

Answer: (C)

$\frac{10^{-15}}{8\epsilon_0}$

Answer 2

Here's how to calculate the volume strain of the sphere:

1. Electric Field at the Surface: For a charged sphere of radius $R = 1 \, m$ and charge $Q = 10^{-2} \, C$:

   $$E = \frac{Q}{4\pi \epsilon_0 R^2} = \frac{10^{-2}}{4\pi \epsilon_0}.$$

2. Electrostatic Pressure: The pressure due to the surface electric field (from Maxwell's stress tensor) is:

   $$P = \frac{1}{2} \epsilon_0 E^2 = \frac{1}{2}\epsilon_0 \left(\frac{Q}{4\pi \epsilon_0 R^2}\right)^2 = \frac{Q^2}{32\pi^2\epsilon_0 R^4}.$$

   For $Q = 10^{-2} \, C$ and $R=1 \, m$:

   $$P = \frac{10^{-4}}{32\pi^2 \epsilon_0}.$$

3. Volume Strain: The volume strain (relative change in volume) produced by this pressure is given by:

   $$\frac{\Delta V}{V} = \frac{P}{K},$$

   where the bulk modulus is

   $$K = \frac{10^{11}}{4\pi^2} \, \frac{N}{m^2}.$$

   Thus,

   $$\frac{\Delta V}{V} = \frac{\displaystyle \frac{10^{-4}}{32\pi^2 \epsilon_0}}{\displaystyle \frac{10^{11}}{4\pi^2}} = \frac{10^{-4}}{32\pi^2 \epsilon_0} \cdot \frac{4\pi^2}{10^{11}} = \frac{4 \times 10^{-4}}{32 \times 10^{11} \epsilon_0}.$$

   Simplifying, $\frac{4}{32} = \frac{1}{8}$ and $10^{-4}/10^{11} = 10^{-15}$, so we have:

   $$\frac{\Delta V}{V} = \frac{10^{-15}}{8\epsilon_0}.$$