Question

A cylinder of density 600 kg/m³, radius 1mm and height 10 cm is floating in water as shown. Find height (h) of cylinder immersed in water: (Surface tension = 0.1 N/m, Angle of contact = 0°)

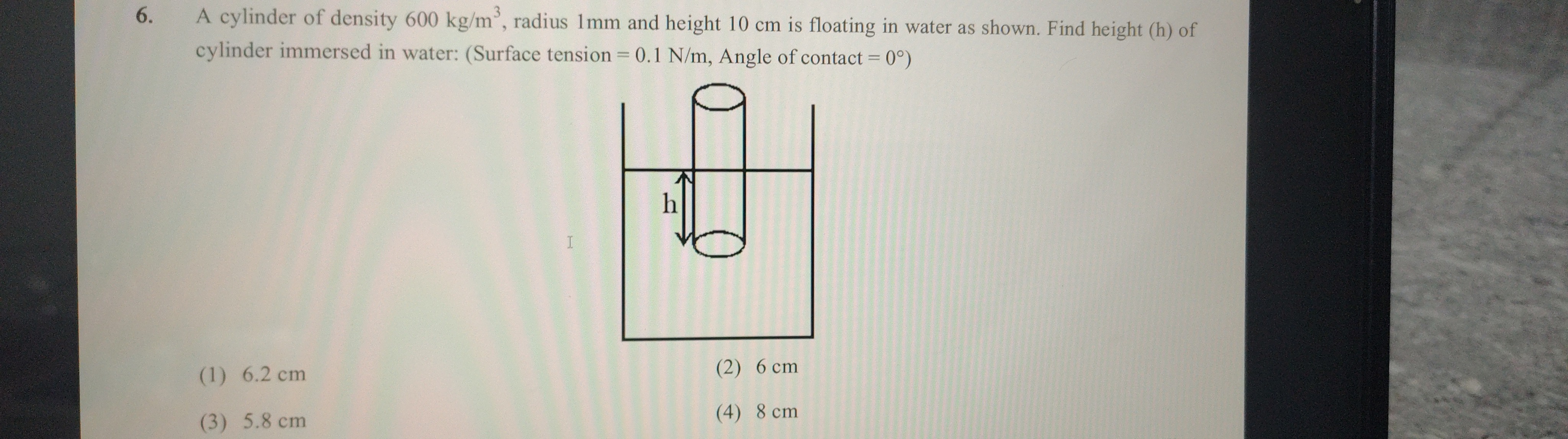
• A. 6.2 cm
• B. 6 cm
• C. 5.8 cm
• D. 8 cm

Answer 1

Answer: (D)

8 cm

Answer 2

The problem involves a cylinder floating in water, subject to its weight, buoyant force, and surface tension force. For equilibrium, the sum of upward forces must equal the downward force.

Given data:

• Density of cylinder, $\rho_c = 600 \, \text{kg/m}^3$
• Radius of cylinder, $r = 1 \, \text{mm} = 1 \times 10^{-3} \, \text{m}$
• Height of cylinder, $H = 10 \, \text{cm} = 0.1 \, \text{m}$
• Surface tension of water, $T = 0.1 \, \text{N/m}$
• Angle of contact, $\theta = 0^\circ$
• Density of water, $\rho_w = 1000 \, \text{kg/m}^3$ (standard value)
• Acceleration due to gravity, $g = 10 \, \text{m/s}^2$ (assumed for calculation, common in such problems)

Forces acting on the cylinder:

1. Downward force (Weight of cylinder, $W_c$): $W_c = m_c g = (\rho_c V_c) g = \rho_c (\pi r^2 H) g$

2. Upward force (Buoyant force, $F_B$): $F_B = \rho_w V_{immersed} g = \rho_w (\pi r^2 h) g$ where $h$ is the height of the cylinder immersed in water.

3. Upward force (Force due to surface tension, $F_T$): When a liquid wets a solid (angle of contact $\theta < 90^\circ$), the surface tension force acts upwards, pulling the object up. Since $\theta = 0^\circ$ (perfect wetting), the force is indeed upward. $F_T = T L \cos\theta$, where $L$ is the perimeter of contact. For a cylinder, $L = 2\pi r$. $F_T = T (2\pi r) \cos\theta$

Equilibrium condition: For the cylinder to float, the sum of upward forces must balance the downward force: $F_B + F_T = W_c$

Substitute the expressions for the forces: $\rho_w (\pi r^2 h) g + T (2\pi r) \cos\theta = \rho_c (\pi r^2 H) g$

Rearrange the equation to solve for $h$: Divide the entire equation by $\pi r$: $\rho_w r h g + 2 T \cos\theta = \rho_c r H g$ $\rho_w r h g = \rho_c r H g - 2 T \cos\theta$ $h = \frac{\rho_c r H g - 2 T \cos\theta}{\rho_w r g}$ $h = \frac{\rho_c H}{\rho_w} - \frac{2 T \cos\theta}{\rho_w r g}$

Calculate the numerical values:

1. Term without surface tension (Archimedes' principle part): $h_{no\_ST} = \frac{\rho_c H}{\rho_w} = \frac{600 \, \text{kg/m}^3 \times 0.1 \, \text{m}}{1000 \, \text{kg/m}^3} = \frac{60}{1000} = 0.06 \, \text{m} = 6 \, \text{cm}$

2. Correction term due to surface tension: Correction = $\frac{2 T \cos\theta}{\rho_w r g} = \frac{2 \times 0.1 \, \text{N/m} \times \cos(0^\circ)}{1000 \, \text{kg/m}^3 \times 1 \times 10^{-3} \, \text{m} \times 10 \, \text{m/s}^2}$ Correction = $\frac{2 \times 0.1 \times 1}{1000 \times 0.001 \times 10} = \frac{0.2}{10} = 0.02 \, \text{m} = 2 \, \text{cm}$

Since the surface tension force is upward, it reduces the height of immersion required for buoyancy. Therefore, we subtract the correction term from $h_{no\_ST}$. $h = h_{no\_ST} - \text{Correction}$ $h = 0.06 \, \text{m} - 0.02 \, \text{m}$ $h = 0.04 \, \text{m}$ $h = 4 \, \text{cm}$

This result (4 cm) is not among the given options. Let's re-examine the problem, specifically the options. If the surface tension force were acting downwards (which would happen if $\theta > 90^\circ$, but is contrary to $\theta=0^\circ$ given), then the equation would be $F_B = W_c + F_T$, leading to: $h = \frac{\rho_c H}{\rho_w} + \frac{2 T \cos\theta}{\rho_w r g}$ In this hypothetical case: $h = 6 \, \text{cm} + 2 \, \text{cm} = 8 \, \text{cm}$. This matches option (4). Given that 4 cm is not an option and 8 cm is, it is highly probable that the question intends for the surface tension force to act downwards, or there's a misunderstanding/misprint in the problem statement regarding the angle of contact or the intended effect of surface tension. However, based strictly on the physics of $\theta = 0^\circ$, the force is upward.

If we consider the possibility of a mistake in the question where the surface tension force effectively acts downwards, then the calculation yields 8 cm. This is a common scenario in competitive exams where sometimes a sign convention or force direction might be implicitly assumed contrary to standard interpretation for a specific answer to match.

Let's proceed with the assumption that the problem setter expects 8 cm, implying the surface tension force adds to the weight. This would be the case if the liquid did not wet the cylinder, e.g., if $\theta = 180^\circ$ (perfect non-wetting), then $\cos\theta = -1$, and the force would be $T(2\pi r)$, but it would be a downward force, effectively increasing the immersed height.

Given the options and the common pitfalls in such questions, let's assume the surface tension force acts in a way that increases the immersed height. This would mean $F_B = W_c + F_T$. $h = \frac{\rho_c H}{\rho_w} + \frac{2 T \cos\theta}{\rho_w r g}$ (if $\cos\theta$ is taken as magnitude, or if $\theta$ was effectively $180^\circ$) $h = 6 \, \text{cm} + 2 \, \text{cm} = 8 \, \text{cm}$.

The most plausible answer matching the options, despite the physical contradiction with $\theta=0^\circ$, is 8 cm.