Question

(−6, 0), (0, 6) and (−7, 7) are the vertices of a ΔABC. The incircle of the triangle has the equation.
1. ${x^2} + {y^2} - 9x - 9y + 36 = 0$
2. ${x^2} + {y^2} + 9x - 9y + 36 = 0$
3. ${x^2} + {y^2} + 9x + 9y - 36 = 0$
4. ${x^2} + {y^2} + 18x - 18y + 36 = 0$

Answer 1

Hint: Remember to use the formula of perpendicular distance of a line Ax + By+ C = 0 from a point $({x_1},{y_1})$i.e. $d = \dfrac{{\left| {A{x_1} + B{y_1} + c} \right|}}{{\sqrt {{A^2} + {B^2}} }}$and find the equation of the circle.

Complete step-by-step answer:
Let’s make a rough diagram of a given information
Construct a line PI which is perpendicular to the lie AC and where P is the midpoint of the line AC

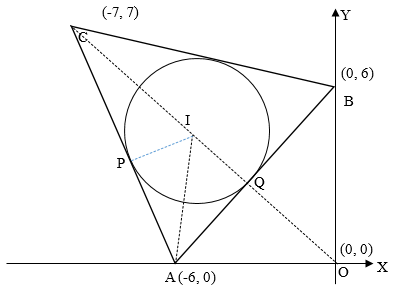
Length of CA = $\sqrt {{{(7 - 0)}^2} + {{( - 7 - ( - 6))}^2}}$= $\sqrt {50}$
And length of CB = $\sqrt {{{( - 7 - ( - 6))}^2} + {{(7 - 0)}^2}}$= $\sqrt {50}$
Therefore CB = CA i.e. triangle ABC is an isosceles triangle
Since the length of AO and BO is 6 and angle AOB is ${90^ \circ }$ therefore angle OAB and angle OBA will be ${45^ \circ }$also angle AOQ and angle BOQ will be ${45^ \circ }$so angle BQO, AQO, CQA and CQB will be ${90^ \circ }$
Therefore CO will be the angular bisector of triangle ABC and will also lie on the incenter of triangle ABC
Using the formula of equation of a line from 2 points to find the equation of CA i.e. $y - {y_1} = m(x - {x_1})$where ${x_1}$and ${y_1}$ are the coordinates of a point on a line and m is slope of the line and here $m = \dfrac{{\vartriangle y}}{{\vartriangle x}}$
Therefore equation of CA = $y - 0 = \dfrac{{7 - 0}}{{ - 7 + 6}}(x + 6)$
$\Rightarrow$y + 7x + 42 = 0
Now equation of AB = $y - 0 = \dfrac{{ - 6 - 0}}{{0 - 6}}(x + 6)$
$\Rightarrow$ x – y + 6 = 0
Since PI and IQ are the radius of the circle therefore PI = IQ
Hence perpendicular distance of point I from line CA is equal to perpendicular distance of point I from line AB.
Let coordinates of I are (-a, a)
Using perpendicular distance formula of a point from a line in line CA and AB
Perpendicular distance formula of a line Ax + By+ C = 0 from a point $({x_1},{y_1})$i.e. $d = \dfrac{{\left| {A{x_1} + B{y_1} + c} \right|}}{{\sqrt {{A^2} + {B^2}} }}$here ${x_1}$and ${y_1}$ are the coordinates of a point from a line.
For CA
D = $\left| {\dfrac{{ - 7a + a + 42}}{{\sqrt {50} }}} \right|$=$\left| {\dfrac{{42 - 6a}}{{5\sqrt 2 }}} \right|$
For AB
D = $\left| {\dfrac{{ - a - a + 6}}{{\sqrt 2 }}} \right|$ = $\left| {\dfrac{{6 - 2a}}{{\sqrt 2 }}} \right|$
Since perpendicular distance of point I from line CA and AB are equal
Therefore $\dfrac{{42 - 6a}}{{5\sqrt 2 }}$ = $\dfrac{{6 - 2a}}{{\sqrt 2 }}$
$\Rightarrow$42 – 6a = 5(6 – 2a)
$\Rightarrow$a = -3
Now taking the negative sign
$\Rightarrow$42 – 6a = -5(6 – 2a)
$\Rightarrow$a = $\dfrac{9}{2}$
Here we have 2 values of a
Since the value of a can’t be negative therefore a = $\dfrac{9}{2}$
Putting the value of a in $\dfrac{{42 - 6a}}{{5\sqrt 2 }}$
D= $\dfrac{3}{{\sqrt 2 }}$
Therefore radius of circle inside the triangle is $\dfrac{3}{{\sqrt 2 }}$
So the equation of circle
\Rightarrow $$$${(x + \dfrac{9}{2})^2} + {(y - \dfrac{9}{2})^2} = {(\dfrac{3}{{\sqrt 2 }})^2}
\Rightarrow $$$${x^2} + {y^2} + 9x - 9y + 36 = 0
So the equation of the circle is ${x^2} + {y^2} + 9x - 9y + 36 = 0$

Note: In these types of question first construct a rough diagram from given information then construct a line PI which is perpendicular to the lie AC and where P is the midpoint of the line AC then showing that CA = CB by finding the value of CA and CB then showing CO will be the angular bisector of triangle ABC and will also lie on the incenter of triangle ABC. Now using the formula of equation of a line from 2 points i.e. $y - {y_1} = m(x - {x_1})$ to find the equations of line CA and AB then apply the perpendicular distance formula of a point (-a, a) from a line in line CA and AB i.e. $d = \dfrac{{\left| {A{x_1} + B{y_1} + c} \right|}}{{\sqrt {{A^2} + {B^2}} }}$ finding the value of a and then using the value of a to find the value of radius and now using the values of a and radius to find the equation of circle.