Question

The question is incomplete as it does not specify what needs to be calculated. However, assuming a typical problem setup for JEE/NEET exams based on the provided diagram, we will calculate the tension in the string and the acceleration of the masses when the system is released from rest with the spring at its natural length.

Assumptions:

1. The horizontal surface is frictionless.
2. The pulley is frictionless and massless.
3. The spring is ideal (massless, obeys Hooke's Law).
4. The system is released from rest, and the spring is initially at its natural length.

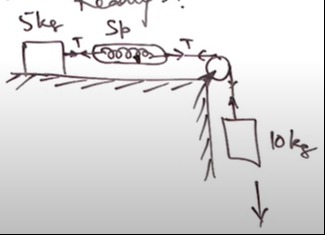
Interpretation of the Diagram: Based on the labels and arrows, the most plausible interpretation is:

• Mass $m_1 = 5kg$ is on a frictionless horizontal surface.
• Mass $m_2 = 10kg$ is hanging vertically.
• A string connects $m_1$ to the pulley. The string passes over the pulley.
• The other end of the string is attached to $m_2$.
• A spring "Sp" is connected between $m_1$ and the pulley.

Let $a$ be the acceleration of $m_1$ to the right and $m_2$ downwards. The tension in the string is $T$. Let $k$ be the spring constant.

Analysis of Forces:

• For mass $m_2$ (10kg): The forces acting on $m_2$ are its weight ($m_2g$) acting downwards and the tension ($T$) acting upwards. Applying Newton's second law: $m_2g - T = m_2a$ $10g - T = 10a$ (Equation 1)

• For mass $m_1$ (5kg): The forces acting on $m_1$ are the tension ($T$) pulling it to the right, and the force exerted by the spring ($F_{sp}$) pulling it to the left (assuming the spring is extended). Applying Newton's second law: $T - F_{sp} = m_1a$ $T - F_{sp} = 5a$ (Equation 2)

• Spring Force ($F_{sp}$): The spring is connected between $m_1$ and the pulley. Assuming the pulley is fixed, the extension of the spring ($x$) is equal to the displacement of $m_1$ from its equilibrium position. The spring force is given by Hooke's Law: $F_{sp} = kx$.

Solving for Acceleration and Tension (Initial State): When the system is released from rest with the spring at its natural length, the initial extension $x=0$, so $F_{sp} = k \times 0 = 0$. Equation 2 becomes: $T - 0 = 5a$ $T = 5a$

Substitute this into Equation 1: $10g - (5a) = 10a$ $10g = 15a$ $a = \frac{10g}{15} = \frac{2g}{3}$

Now, find the tension $T$: $T = 5a = 5 \times \frac{2g}{3} = \frac{10g}{3}$

Using $g \approx 9.8 \, m/s^2$ or $g \approx 10 \, m/s^2$: If $g \approx 10 \, m/s^2$: $a = \frac{2 \times 10}{3} = \frac{20}{3} \, m/s^2 \approx 6.67 \, m/s^2$ $T = \frac{10 \times 10}{3} = \frac{100}{3} \, N \approx 33.3 \, N$

If $g \approx 9.8 \, m/s^2$: $a = \frac{2 \times 9.8}{3} = \frac{19.6}{3} \, m/s^2 \approx 6.53 \, m/s^2$ $T = \frac{10 \times 9.8}{3} = \frac{98}{3} \, N \approx 32.67 \, N$

Since no specific question or options are provided, we cannot select an answer. However, the derived values for acceleration and tension are standard results for this type of problem.

Answer 1

The question is incomplete. Based on standard interpretations, the initial acceleration of the system is $a = \frac{2g}{3}$ and the initial tension in the string is $T = \frac{10g}{3}$.

Answer 2

The problem describes a system of two masses connected by a string over a pulley and a spring. Assuming the system is released from rest with the spring at its natural length, we apply Newton's second law to each mass. The tension in the string is the same throughout. The spring force acts on the 5kg mass and the pulley. For the initial moment, the spring force is zero. This allows us to set up two equations with two unknowns (tension $T$ and acceleration $a$), which are then solved.