Question

$5g$ of water rises in the bore of the capillary tube when it is dipped in water. If the radius of the bore capillary tube is doubled, the mass of water that rises in the capillary tube above the outside water level is
(A) $1.5g$
(B) $10g$
(C) $5g$
(D) $15g$

Answer 1

Hint We know that the pressure at a point $A$ and $B$ in the diagram is the same. The pressure drop when going downwards through the meniscus from the point $A$ is $\dfrac{{2T}}{R}$, where $T$ is the surface tension of water and $R$ is the radius of the meniscus. This pressure drop is compensated by the pressure of the water column. Once we balance these, we will get our required solution.

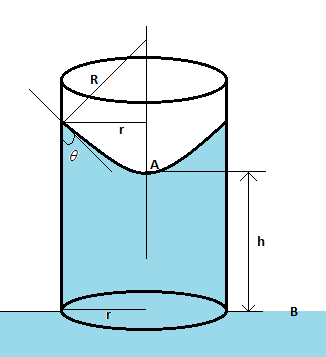
Complete Step by step solution The height of the water column is calculated from the equation $\rho gh = \dfrac{{2T}}{R}$, where $\rho$ is the density of water, $h$ is the height of the water column, $g$ is the acceleration due to gravity, $T$ is the surface tension of water, and $R$ is the radius of the meniscus. Now from the figure, we get $\cos \theta = \dfrac{R}{r}$, i.e. $R = r\cos \theta$ such that the above equation becomes $\rho gh = \dfrac{{2T}}{{r\cos \theta }}$.
Also, we need to find the mass of the water column in terms of the height and radius of the cylinder. If $M$ be the mass of the water column, then $M = \rho V = \rho (\pi {r^2}h)$. Substituting $h$ from the above equation, we get $h = \dfrac{M}{{\rho \pi {r^2}}}$.
Replacing $h$, in the equation $\rho gh = \dfrac{{2T}}{{r\cos \theta }}$, we get $\dfrac{{\rho gM}}{{\rho \pi {r^2}}} = \dfrac{{2T}}{{r\cos \theta }}$.
Cancelling terms and taking all constants on one side we get, $\dfrac{M}{r} = \dfrac{{2\pi T}}{{g\cos \theta }} = const.$
Now according to the given question, the mass of water in the capillary tube is $5grams$, and the radius $r$ gets doubled.
$\Rightarrow \dfrac{M}{r} = const. = \dfrac{{{M_1}}}{{{r_1}}} = \dfrac{{{M_2}}}{{{r_2}}}$,
$\therefore \dfrac{{5grams}}{{{r_1}}} = \dfrac{{{M_2}}}{{2{r_1}}}$, or ${M_2} = 10grams$.

Therefore the correct option is an option (B).

Note Here we take the pressure drop as $\dfrac{{2T}}{R}$ and not $\dfrac{{4T}}{R}$, since the water column has only a single layer. In the case of bubbles, the pressure difference between the concave and the convex sides is $\dfrac{{4T}}{R}$. The concave side of a bubble has more pressure than the concave side.