Question

Let $A = \begin{bmatrix} 1 & a & 0 \\ 0 & 1 & a \\ a & 0 & 1 \end{bmatrix}, X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}, B = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$ and $AX = B$, then the system of equations has infinite number of solutions, then

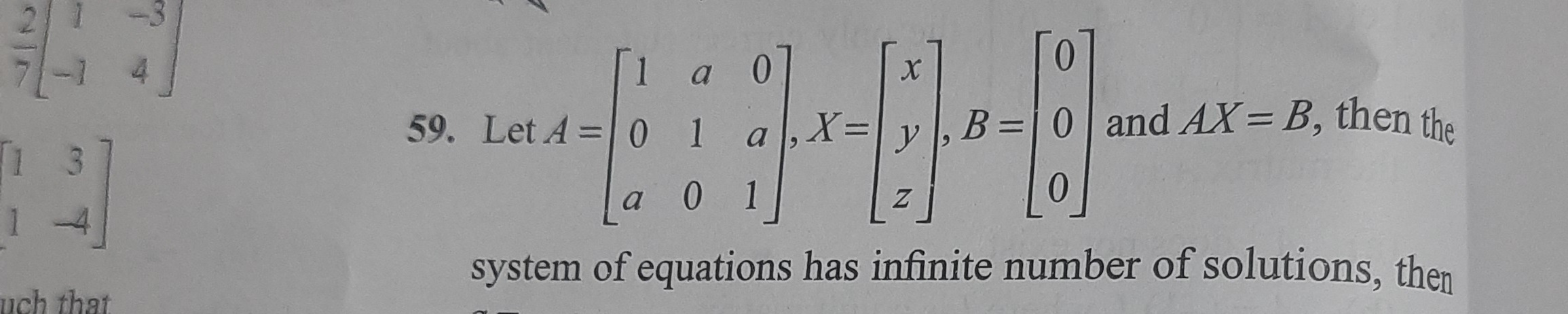
• A. -1
• B. 0
• C. 1
• D. 2

Answer 1

Answer: (A)

a = -1

Answer 2

For the system $AX = B$ to have infinitely many solutions, the matrix $A$ must be singular. This means:

$$\det(A) = 0$$

Given:

$$A = \begin{bmatrix} 1 & a & 0 \\ 0 & 1 & a \\ a & 0 & 1 \end{bmatrix}$$

Compute the determinant:

$$\det(A) = 1\begin{vmatrix} 1 & a \\ 0 & 1 \end{vmatrix} - a \begin{vmatrix} 0 & a \\ a & 1 \end{vmatrix} + 0\begin{vmatrix} 0 & 1 \\ a & 0 \end{vmatrix}$$ $$= 1(1 \cdot 1 - a \cdot 0) - a (0 \cdot 1 - a \cdot a)$$ $$= 1 - a(-a^2)$$ $$= 1 + a^3$$

Setting $\det(A) = 0$:

$$1 + a^3 = 0 \quad \Longrightarrow \quad a^3 = -1 \quad \Longrightarrow \quad a = -1.$$

Thus, the system has infinitely many solutions when $a = -1$.

The homogeneous system $AX = B$ has infinite solutions if the determinant of $A$ is zero. Calculating $\det(A)$ gives $1 + a^3$, which is zero when $a = -1$.