Question
Question: For any real number b, let f(b) denotes the maximum of |$\sin x + \frac{2}{3 + \sin x} + b$| $\foral...
For any real number b, let f(b) denotes the maximum of |sinx+3+sinx2+b| ∀x∈R. Then the minimum value of f(b) ∀b∈R is:
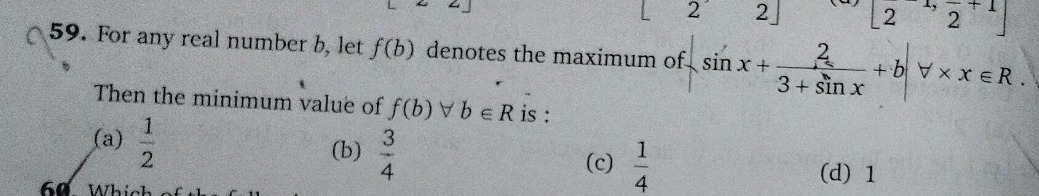
A
21
B
43
C
41
D
1
Answer
43
Explanation
Solution
Let y=3+sinx. Since −1≤sinx≤1, the range of y is [2,4]. Let g(y)=y+y2. The derivative g′(y)=1−y22>0 for y∈[2,4], so g(y) is increasing. The range of g(y) on [2,4] is [g(2),g(4)]=[2+22,4+42]=[3,29]. The expression is ∣g(y)−3+b∣. Let k=g(y)−3. The range of k is [3−3,29−3]=[0,23]. We want to find the minimum of f(b)=maxk∈[0,3/2]∣k+b∣. This is equivalent to finding the minimum of maxA∈[b,b+3/2]∣A∣. This maximum is minimized when the interval [b,b+3/2] is centered at 0. The midpoint is b+43. Setting b+43=0, we get b=−43. The interval becomes [−43,43], and the maximum value of ∣A∣ is 43.
