Question
Question: The value of $\int_{0}^{\pi/2}\frac{dx}{(4cos^2x+9sin^2x)^2}$ is equal to...
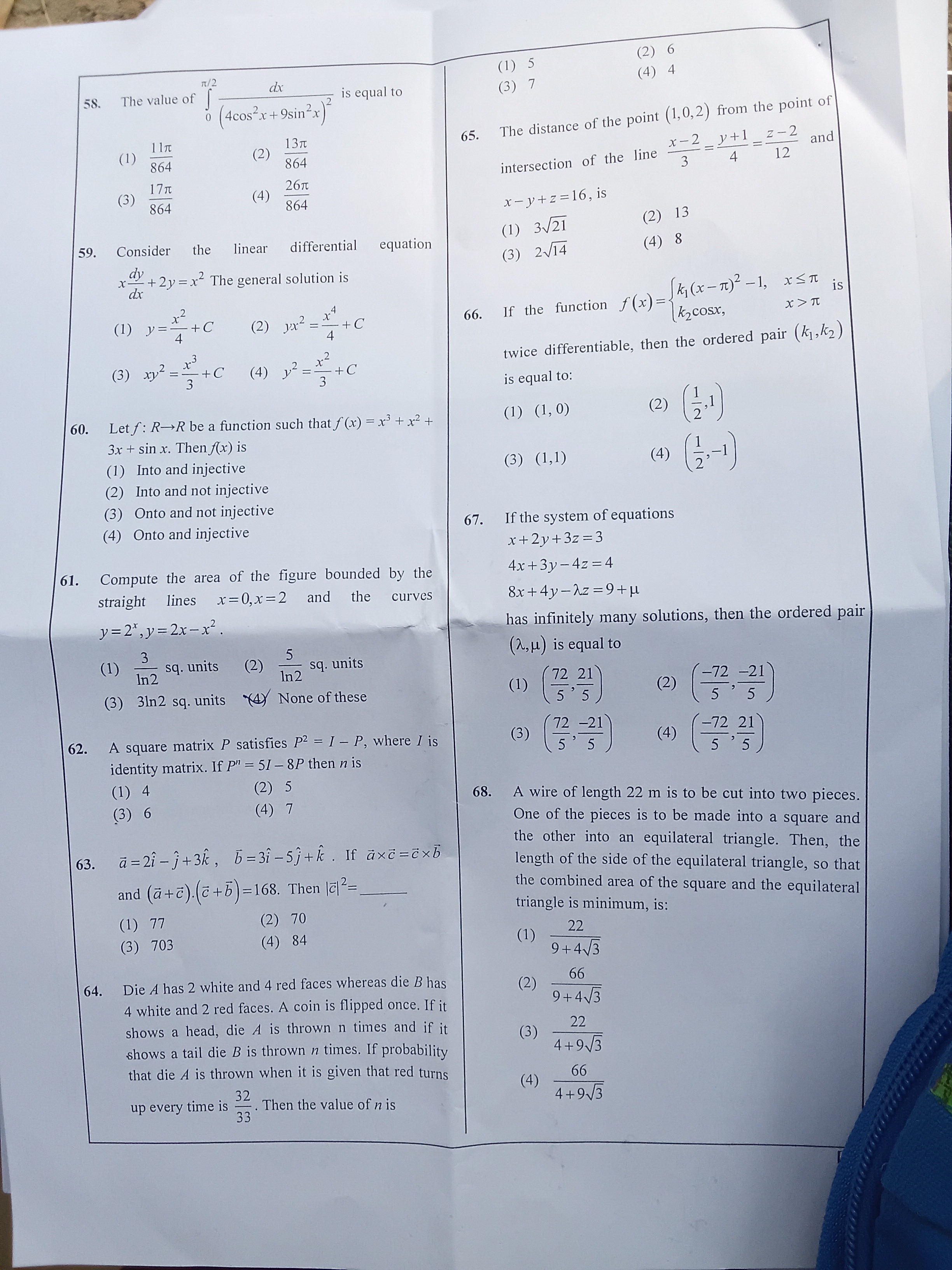
The value of ∫0π/2(4cos2x+9sin2x)2dx is equal to
A
(1) 86411π
B
(2) 86413π
C
(3) 86417π
D
(4) 86426π
Answer
(2) 86413π
Explanation
Solution
We can use the formula ∫0π/2(a2cos2x+b2sin2x)2dx=4a3b3π(a2+b2). Here, a2=4 and b2=9, so a=2 and b=3. Substituting these values into the formula: 4(23)(33)π(4+9)=4(8)(27)π(13)=4(216)13π=86413π
