Question

The deflection in galvanometer falls to $(\frac{1}{4})^{th}$ when it is shunted by 3 $\Omega$. If additiona shunt of 2 $\Omega$ is connected to earlier shunt, the deflection in galvanometer falls to

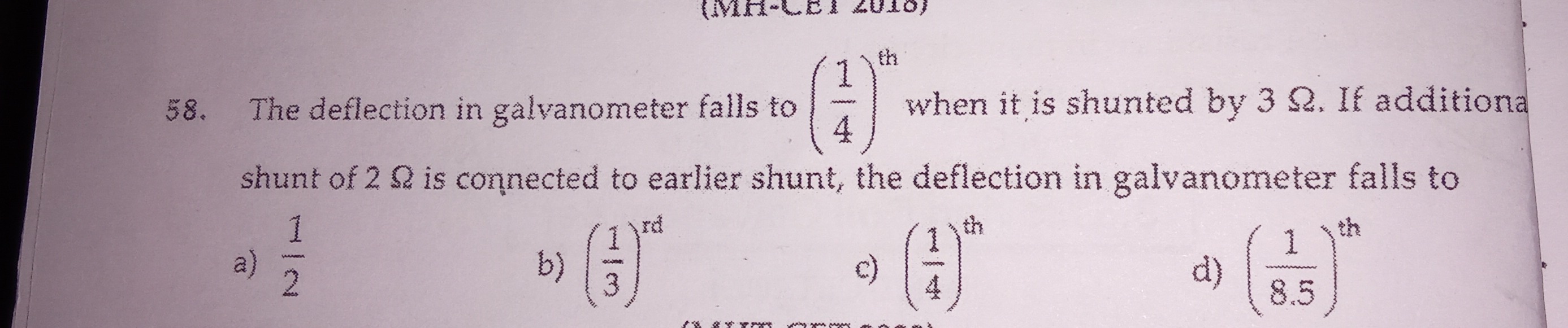
• A. $\frac{1}{2}$
• B. $(\frac{1}{3})^{rd}$
• C. $(\frac{1}{4})^{th}$
• D. $(\frac{1}{8.5})^{th}$

Answer 1

Answer: (D)

Option d) $(\frac{1}{8.5})^{th}$

Answer 2

Solution:

Let the internal resistance of the galvanometer be $G$. The deflection (proportional to the current through the galvanometer) falls to $\frac{1}{4}$ of its full-scale value when shunted by $3\,\Omega$. In this configuration, by current division:

$$\frac{3}{G+3} = \frac{1}{4}$$

Solving:

$$3 = \frac{G+3}{4} \quad \Longrightarrow \quad G+3=12 \quad \Longrightarrow \quad G=9\,\Omega.$$

Now, an additional $2\,\Omega$ shunt is connected in parallel with the $3\,\Omega$ shunt. Their combined (parallel) resistance is:

$$R_{\text{shunt}} = \frac{3\times2}{3+2} = \frac{6}{5}\,\Omega.$$

The current division now gives the fraction of the total current through the galvanometer as:

$$\text{Fraction } = \frac{R_{\text{shunt}}}{G + R_{\text{shunt}}} = \frac{\frac{6}{5}}{9 + \frac{6}{5}} = \frac{\frac{6}{5}}{\frac{45}{5} + \frac{6}{5}} = \frac{6}{51} = \frac{2}{17}.$$

Notice that $\frac{2}{17}$ is equivalent to $\frac{1}{8.5}$.

Core Explanation:

1. Use current division: $\frac{3}{G+3}=\frac{1}{4}$ to find $G=9\,\Omega$.
2. The combined resistance of 3 Ω and 2 Ω in parallel is $\frac{6}{5}\,\Omega$.
3. New fraction of current: $\frac{6/5}{9+6/5}=\frac{2}{17} = \frac{1}{8.5}$.