Question
Question: If $\frac{1}{6}$sin$\theta$, cos$\theta$, tan$\theta$ are in G.P. then $\theta$ =...
If 61sinθ, cosθ, tanθ are in G.P. then θ =
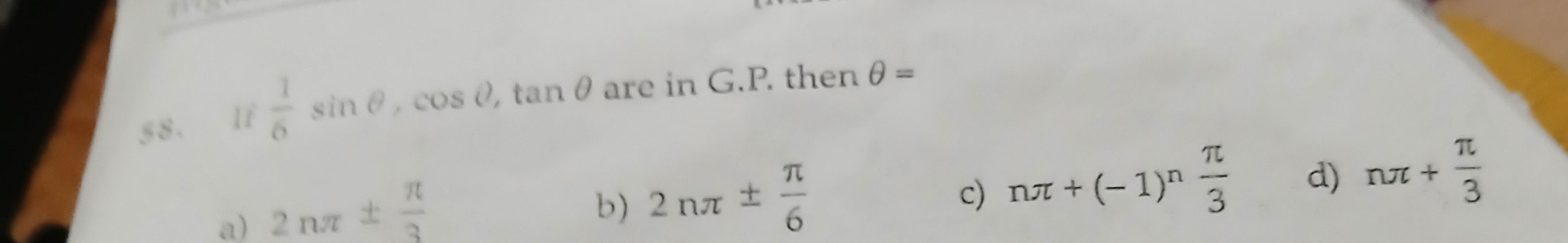
A
2nπ ± 3π
B
2nπ ± 6π
C
nπ+(-1)^{n}$$\frac{\pi}{3}
D
nπ+3π
Answer
Option (a)
Explanation
Solution
For numbers a,b,c in G.P. we have b2=ac. Here,
a=61sinθ,b=cosθ,c=tanθ.So,
cos2θ=61sinθ⋅tanθ.Since tanθ=cosθsinθ, we get:
cos2θ=61⋅cosθsin2θ.Multiply both sides by cosθ:
cos3θ=61sin2θ.Multiply by 6:
6cos3θ=sin2θ.Using the identity sin2θ=1−cos2θ:
6cos3θ=1−cos2θ.Rearrange:
6cos3θ+cos2θ−1=0.Let x=cosθ, then:
6x3+x2−1=0.Testing x=21:
6(21)3+(21)2−1=6(81)+41−1=43+41−1=0.Thus, cosθ=21, which gives:
θ=2nπ±3π,n∈Z.Explanation (Minimal):
Numbers are in G.P. ⇒ b2=ac leads to 6cos3θ=sin2θ. Substitute sin2θ=1−cos2θ to form a cubic. x=21 is a solution, so cosθ=21 and hence θ=2nπ±3π.
