Question
Question: Complete set of values of $m$, for which function $f(x)=3+mx+e^{-x}$ is always decreasing, is...
Complete set of values of m, for which function f(x)=3+mx+e−x is always decreasing, is
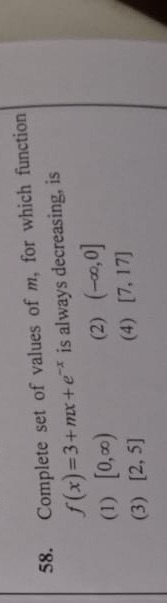
[0,∞)
(−∞,0]
[2,5]
[7,17]
(2)
Solution
To determine the values of m for which the function f(x)=3+mx+e−x is always decreasing, we need to ensure that its first derivative, f′(x), is less than or equal to zero for all x∈R.
Step 1: Find the first derivative of the function f(x).
Given f(x)=3+mx+e−x.
Differentiating f(x) with respect to x:
f′(x)=dxd(3)+dxd(mx)+dxd(e−x)
f′(x)=0+m(1)+e−x(−1)
f′(x)=m−e−x
Step 2: Set the condition for the function to be always decreasing.
For f(x) to be always decreasing, we must have f′(x)≤0 for all x∈R.
So, we set up the inequality:
m−e−x≤0
Step 3: Solve the inequality for m.
Rearranging the inequality, we get:
m≤e−x
This inequality must hold true for all values of x∈R.
To satisfy m≤e−x for all x, m must be less than or equal to the minimum value that e−x can take.
Let's analyze the behavior of the function g(x)=e−x:
- As x→∞, e−x→0.
- As x→−∞, e−x→∞.
The range of e−x is (0,∞). This means e−x is always positive and can take any value greater than 0. However, it never actually reaches 0. The infimum (greatest lower bound) of the set of values e−x can take is 0.
For m≤e−x to hold for all x, m must be less than or equal to this infimum.
Therefore, m≤0.
Step 4: Express the set of values of m. The complete set of values of m for which f(x) is always decreasing is m∈(−∞,0].
