Question

If $\cos^{-1}x - \cos^{-1}\frac{y}{2} = \alpha$, where $1 \leq x \leq 1, -2 \leq y \leq 2, x \leq \frac{y}{2}$ then for all x, y, $4x^2 - 4xy \cos \alpha + y^2$ is equal to :

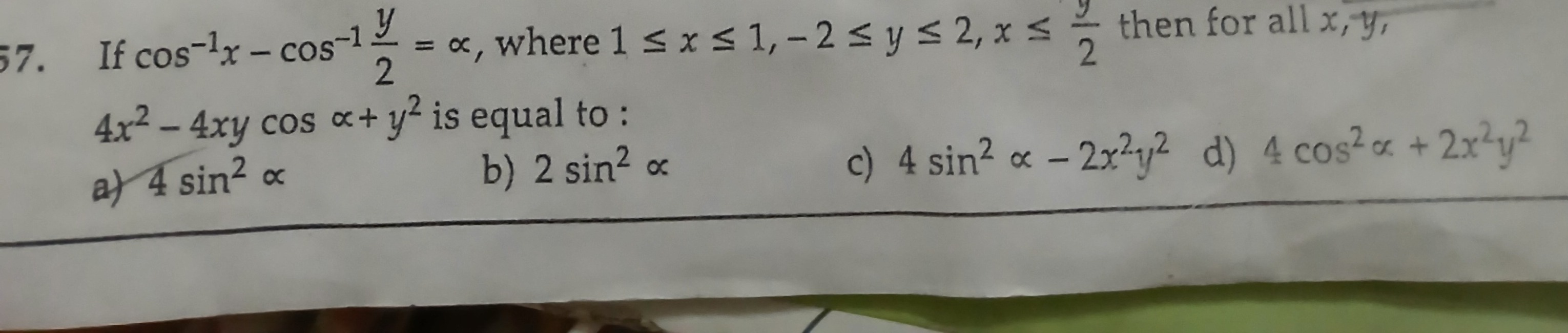
• A. $4 \sin^2 \alpha$
• B. $2 \sin^2 \alpha$
• C. $4 \sin^2 \alpha - 2x^2y^2$
• D. $4 \cos^2 \alpha + 2x^2y^2$

Answer 1

Answer: (A)

$4\sin^2\alpha$

Answer 2

We are given:

$$\cos^{-1}x - \cos^{-1}\frac{y}{2} = \alpha$$

Let

$$A = \cos^{-1}x \quad \text{and} \quad B = \cos^{-1}\frac{y}{2},$$

so that

$$A - B = \alpha \quad \Rightarrow \quad A = \alpha + B.$$

Then,

$$x = \cos A = \cos(\alpha+B) = \cos\alpha\cos B - \sin\alpha\sin B.$$

Since $\cos B = \frac{y}{2}$, substitute:

$$x = \cos\alpha \cdot \frac{y}{2} - \sin\alpha\sin B.$$

Now, rewrite the target expression:

$$4x^2 - 4xy \cos \alpha + y^2.$$

Notice that completing the square for the first two terms gives:

$$(2x - y\cos\alpha)^2 = 4x^2 - 4xy\cos\alpha + y^2\cos^2\alpha.$$

Thus,

$$4x^2 - 4xy\cos\alpha + y^2 = (2x - y\cos\alpha)^2 + y^2\sin^2\alpha.$$

Next, express $2x - y\cos\alpha$ using our expression for $x$:

$$2x = 2\left(\frac{y\cos\alpha}{2} - \sin\alpha\sin B\right) = y\cos\alpha - 2\sin\alpha\sin B.$$

So,

$$2x - y\cos\alpha = -2\sin\alpha\sin B.$$

Substitute back:

$$(2x - y\cos\alpha)^2 = 4\sin^2\alpha\sin^2B.$$

Also, note that $y = 2\cos B$ (since $\cos B = \frac{y}{2}$), hence:

$$y^2\sin^2\alpha = 4\cos^2B\sin^2\alpha.$$

Now, the expression becomes:

$$4\sin^2\alpha\sin^2B + 4\sin^2\alpha\cos^2B = 4\sin^2\alpha(\sin^2B+\cos^2B).$$

Since $\sin^2B+\cos^2B=1$:

$$4\sin^2\alpha(\sin^2B+\cos^2B)=4\sin^2\alpha.$$