Question

Let $A = \begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix}$, then the number of column

$X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}$ such that $AX = \lambda X$ for some scalar $\lambda$ is

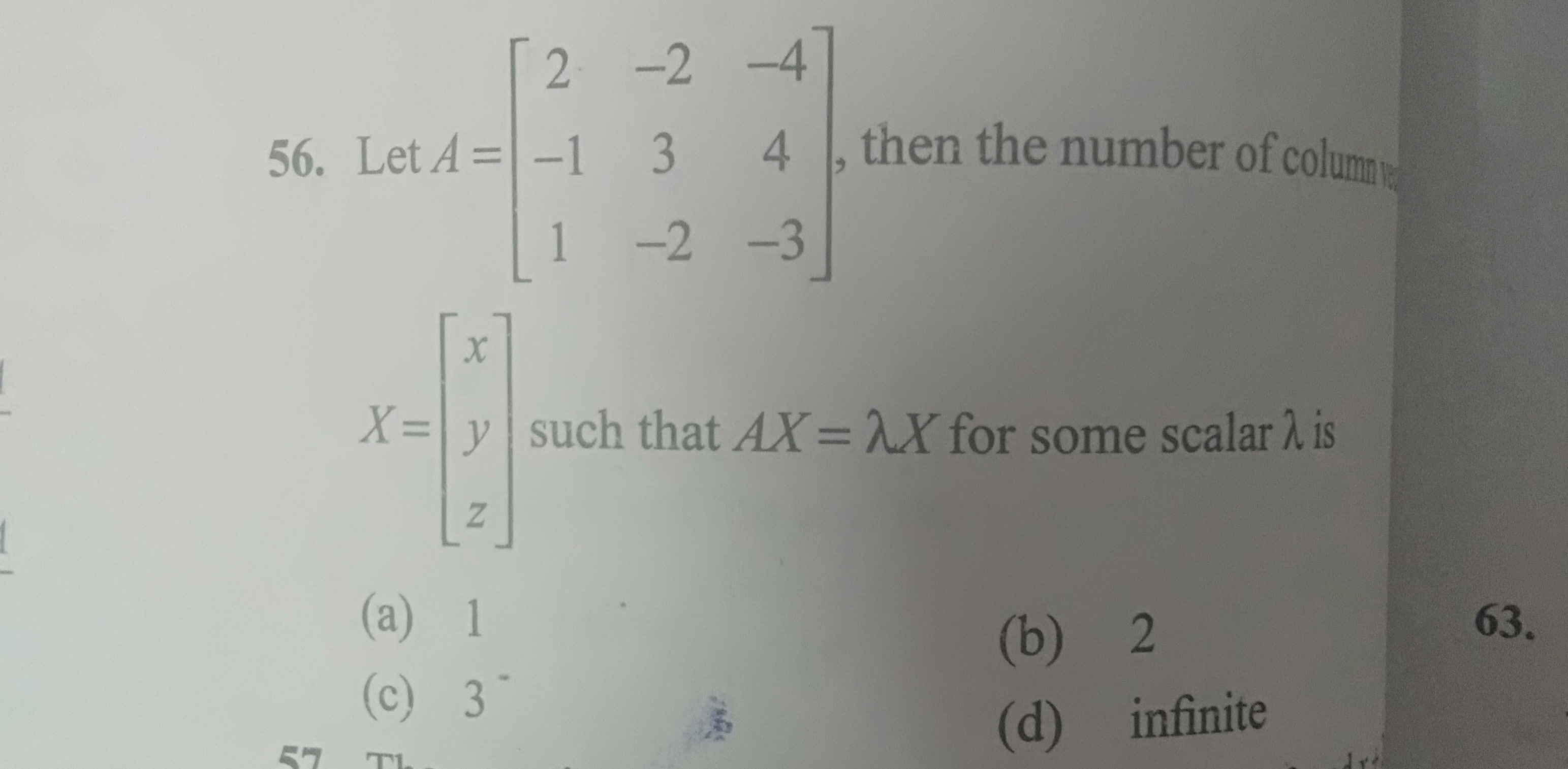
• A. 1
• B. 2
• C. 3
• D. infinite

Answer 1

Answer: (D)

infinite

Answer 2

We are given

$$A=\begin{bmatrix} 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end{bmatrix},$$

and need to find the number of nonzero column vectors $X=\begin{bmatrix} x\\ y\\ z \end{bmatrix}$ such that

$$AX = \lambda X$$

for some scalar $\lambda$.

This equation represents the eigenvalue equation. To see how many eigenvectors (nonzero solutions) exist, we first find the eigenvalues by solving the characteristic equation $\det(A-\lambda I)=0$.

We have:

$$A-\lambda I = \begin{bmatrix} 2-\lambda & -2 & -4 \\ -1 & 3-\lambda & 4 \\ 1 & -2 & -3-\lambda \end{bmatrix}.$$

A computation shows that the characteristic polynomial factors as:

$$-\lambda(\lambda-1)^2=0.$$

Thus, the eigenvalues are:

• $\lambda = 0$ (simple)
• $\lambda = 1$ (double)

For each eigenvalue, if the corresponding eigenspace is nontrivial (i.e. of positive dimension), then there are infinitely many eigenvectors (any nonzero scalar multiple of an eigenvector is again an eigenvector).

Since both eigenspaces (regardless of dimension) are nontrivial, there are infinitely many column vectors $X$ satisfying $AX=\lambda X$.