Question
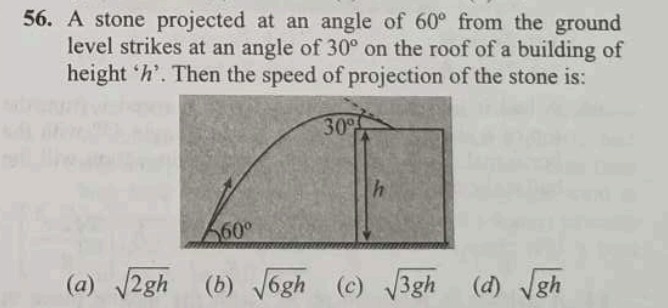
Question: A stone projected at an angle of 60° from the ground level strikes at an angle of 30° on the roof of...
A stone projected at an angle of 60° from the ground level strikes at an angle of 30° on the roof of a building of height 'h'. Then the speed of projection of the stone is:
2gh
6gh
3gh
gh
3gh
Solution
Let the initial speed of projection be v0 and the angle of projection be θ=60∘. The horizontal component of initial velocity is v0x=v0cos60∘=2v0, and the vertical component is v0y=v0sin60∘=23v0.
At height h, the horizontal component of velocity remains constant: vx=v0x=2v0. The vertical component of velocity at height h, vy, can be found using vy2=v0y2−2gh. vy2=(23v0)2−2gh=43v02−2gh.
The stone strikes the roof at an angle of 30∘ with the horizontal. Therefore, tan(30∘)=vxvy. vy=vxtan(30∘)=(2v0)(31)=23v0.
Squaring vy: vy2=(23v0)2=12v02.
Equating the two expressions for vy2: 12v02=43v02−2gh 2gh=43v02−12v02=129v02−v02=128v02=32v02.
Solving for v02: v02=23×2gh=3gh. Therefore, the speed of projection v0=3gh.
