Question

A quantity of 34 g sample of $BaO_2$ is heated to 1000 K in a closed and rigid evacuated vessel of 8.21 L capacity. What percentage of peroxide is converted into oxide? (Ba = 138)

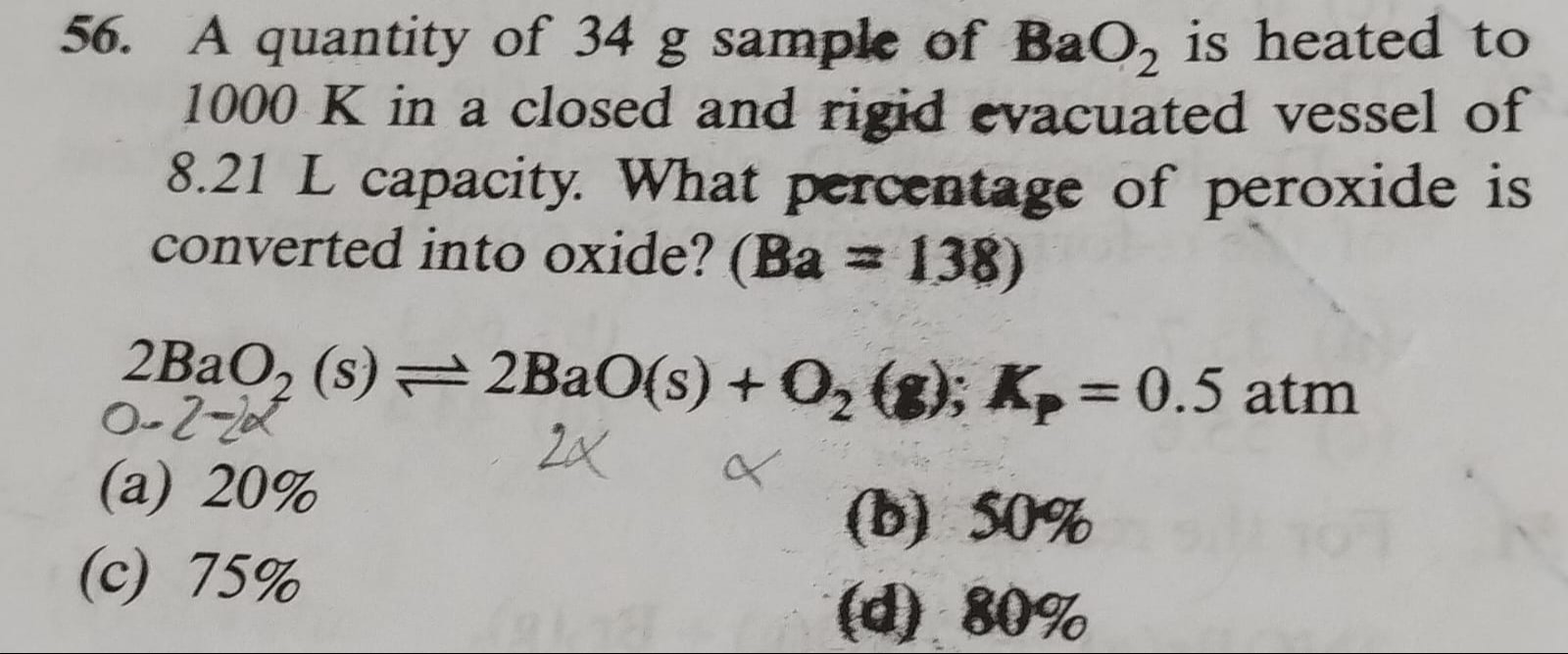
• A. 20%
• B. 50%
• C. 75%
• D. 80%

Answer 1

Answer: (B)

50%

Answer 2

The equilibrium constant $K_p$ for the reaction $2BaO_2(s) \rightleftharpoons 2BaO(s) + O_2(g)$ is given by $K_p = P_{O_2}$. Given $K_p = 0.5$ atm, the partial pressure of $O_2$ at equilibrium is $P_{O_2} = 0.5$ atm. Using the ideal gas law, $PV = nRT$, we calculate the moles of $O_2$ produced at equilibrium: $n_{O_2} = \frac{P_{O_2}V}{RT} = \frac{(0.5 \text{ atm})(8.21 \text{ L})}{(0.0821 \text{ L atm/mol K})(1000 \text{ K})} = 0.05$ mol. The molar mass of $BaO_2$ is $138 + 2 \times 16 = 170$ g/mol. The initial mass of $BaO_2$ is 34 g, so the initial moles are: Initial moles of $BaO_2 = \frac{34 \text{ g}}{170 \text{ g/mol}} = 0.2$ mol. From the stoichiometry of the reaction ($2BaO_2 \rightarrow 2BaO + O_2$), 2 moles of $BaO_2$ decompose to produce 1 mole of $O_2$. Therefore, if $0.05$ mol of $O_2$ is produced, the moles of $BaO_2$ reacted are $2 \times 0.05 = 0.1$ mol. The percentage conversion of $BaO_2$ is calculated as: Percentage conversion = $\frac{\text{moles of } BaO_2 \text{ reacted}}{\text{initial moles of } BaO_2} \times 100\% = \frac{0.1 \text{ mol}}{0.2 \text{ mol}} \times 100\% = 50\%$.