Question
Question: The principal value of $\tan^{-1}\left(\cot\left(\frac{43\pi}{4}\right)\right)$ is...
The principal value of tan−1(cot(443π)) is
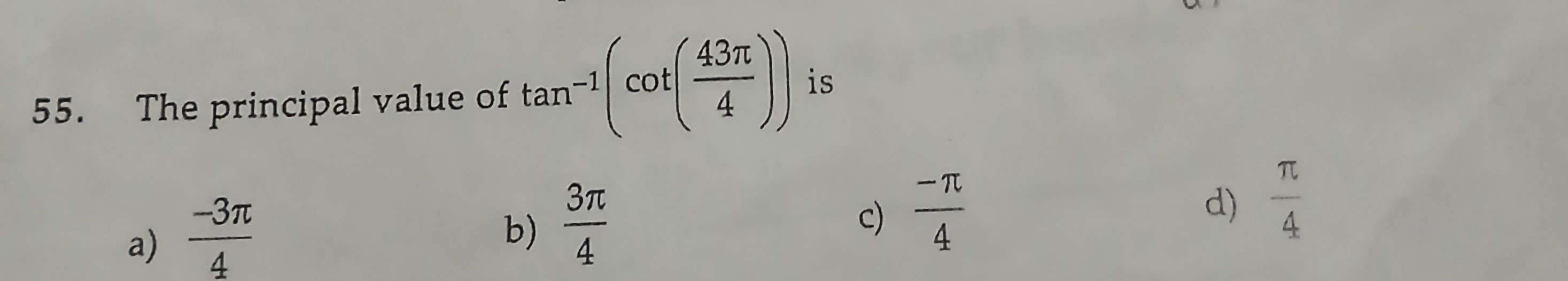
A
4−3π
B
43π
C
4−π
D
4π
Answer
4−π
Explanation
Solution
-
Write
cot(443π)=tan(2π−443π)=tan(−441π). -
Since the principal value of tan−1 lies in (−2π,2π), we find an equivalent angle:
−441π+10π=−441π+440π=−4π. -
Thus,
tan−1(cot(443π))=−4π.
Explanation (Minimal): Express cot(443π) as tan(−441π). Adjust −441π by adding 10π (due to the π period of tan) to yield −4π which lies in (−2π,2π).
