Question

The number of gas molecules effusing per second unit area through an orifice on the wall of the container is $\frac{1}{4}.N^*.u_{av}$, where $N^*$ is the number of molecules per unit volume. What is this number under STP conditions for nitrogen gas?

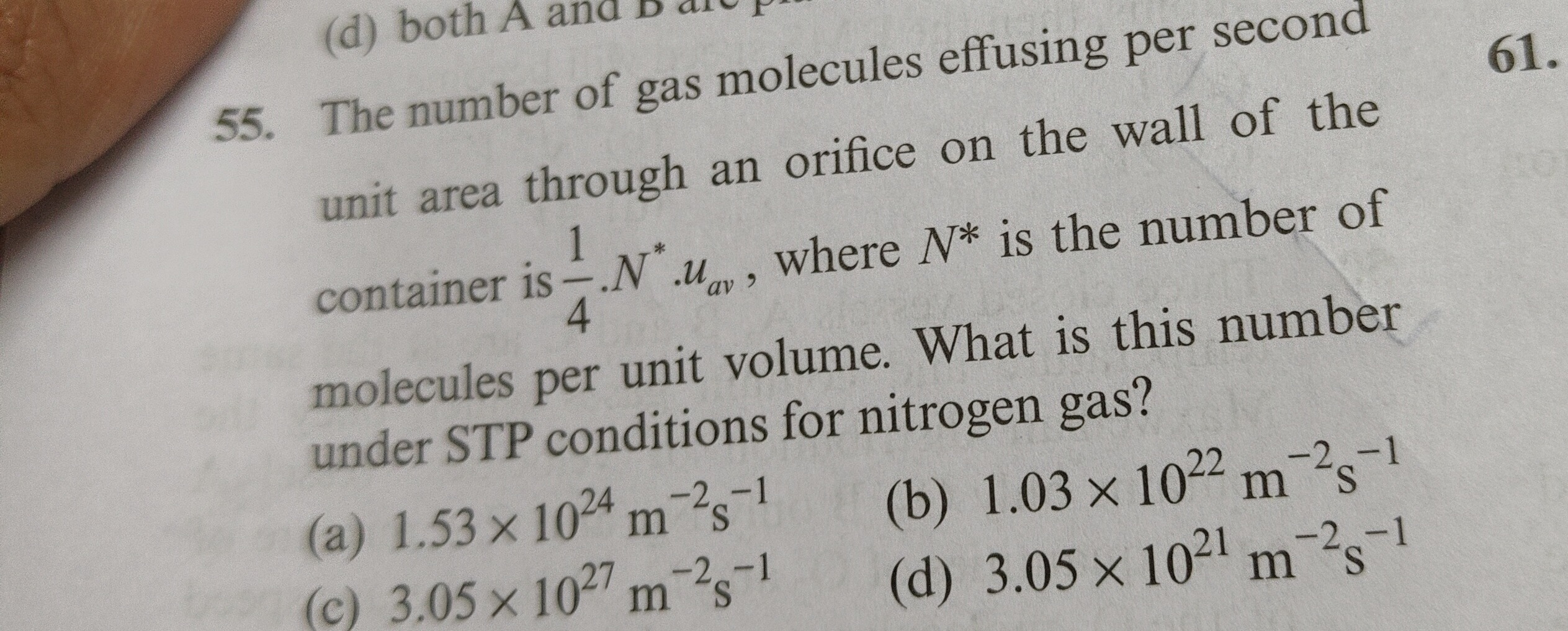
• A. 1.53 x $10^{24}$ $m^{-2}s^{-1}$
• B. 1.03 × $10^{22}$ $m^{-2}s^{-1}$
• C. 3.05 x $10^{27}$ $m^{-2}s^{-1}$
• D. 3.05 × $10^{21}$ $m^{-2}s^{-1}$

Answer 1

Answer: (C)

3.05 x $10^{27}$ $m^{-2}s^{-1}$

Answer 2

At STP, $T = 273.15$ K and $P = 1.013 \times 10^5$ Pa. The number density $N^*$ is calculated using $P = N^*kT$: $N^* = \frac{P}{kT} = \frac{1.013 \times 10^5 \text{ Pa}}{(1.38 \times 10^{-23} \text{ J/K}) \times (273.15 \text{ K})} \approx 2.687 \times 10^{25} \text{ m⁻³}$. The average speed $u_{av}$ for nitrogen (M = 0.028 kg/mol) is: $u_{av} = \sqrt{\frac{8RT}{\pi M}} = \sqrt{\frac{8 \times 8.314 \times 273.15}{\pi \times 0.028}} \approx 454.26 \text{ m/s}$. The effusion rate is $\frac{1}{4}N^*u_{av} = \frac{1}{4} \times (2.687 \times 10^{25}) \times 454.26 \approx 3.05 \times 10^{27} \text{ m⁻²s⁻¹}$.