Question

Let $f(x) = \begin{cases} (1+3x)^{\frac{1}{x}}, & x \neq 0 \\ e^3, & x = 0 \end{cases}$ Discuss the continuity of $f(x)$ at (i) x = 0, (ii) x = 1.

Answer 1

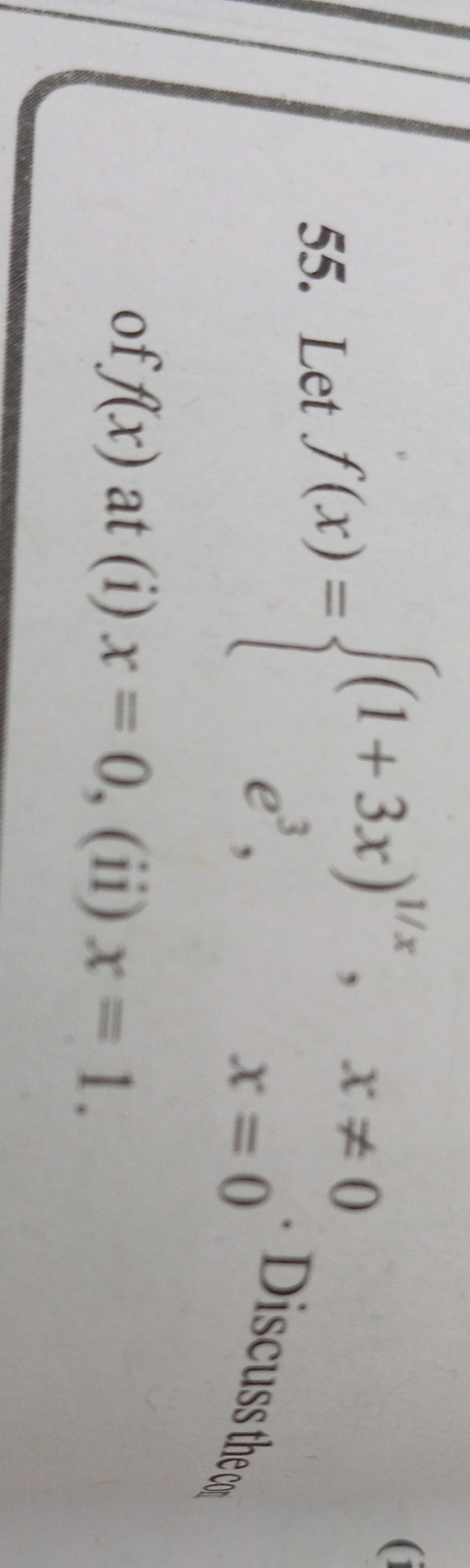
f(x) is continuous at x=0 and x=1.

Answer 2

To discuss the continuity of $f(x)$ at a point $x=a$, we need to check if the following three conditions are satisfied:

1. $f(a)$ is defined.
2. $\lim_{x \to a} f(x)$ exists.
3. $\lim_{x \to a} f(x) = f(a)$.

Part (i): Continuity at x = 0

1. Value of the function at x = 0:
   From the definition of $f(x)$, we are given $f(0) = e^3$.

2. Limit of the function as x approaches 0:
   We need to find $\lim_{x \to 0} f(x) = \lim_{x \to 0} (1+3x)^{\frac{1}{x}}$.
   This is an indeterminate form of type $1^\infty$. We use the standard limit formula $\lim_{x \to 0} (1+ax)^{\frac{1}{x}} = e^a$.
   In this case, $a=3$.
   So, $\lim_{x \to 0} (1+3x)^{\frac{1}{x}} = e^3$.

3. Comparison:
   Since $\lim_{x \to 0} f(x) = e^3$ and $f(0) = e^3$, we have $\lim_{x \to 0} f(x) = f(0)$.
   Therefore, $f(x)$ is continuous at $x=0$.

Part (ii): Continuity at x = 1

1. Value of the function at x = 1:
   For $x \neq 0$, $f(x) = (1+3x)^{\frac{1}{x}}$.
   So, $f(1) = (1+3(1))^{\frac{1}{1}} = (1+3)^1 = 4^1 = 4$.

2. Limit of the function as x approaches 1:
   We need to find $\lim_{x \to 1} f(x) = \lim_{x \to 1} (1+3x)^{\frac{1}{x}}$.
   Since $x=1$ is not a point of discontinuity for the expression $(1+3x)^{\frac{1}{x}}$ (the base $1+3x$ is positive and the exponent $\frac{1}{x}$ is well-defined at $x=1$), we can directly substitute $x=1$.
   $\lim_{x \to 1} (1+3x)^{\frac{1}{x}} = (1+3(1))^{\frac{1}{1}} = (1+3)^1 = 4^1 = 4$.

3. Comparison:
   Since $\lim_{x \to 1} f(x) = 4$ and $f(1) = 4$, we have $\lim_{x \to 1} f(x) = f(1)$.
   Therefore, $f(x)$ is continuous at $x=1$.

The function $f(x)$ is continuous at both $x=0$ and $x=1.