Question

$\int sin^4 x \, dx =$

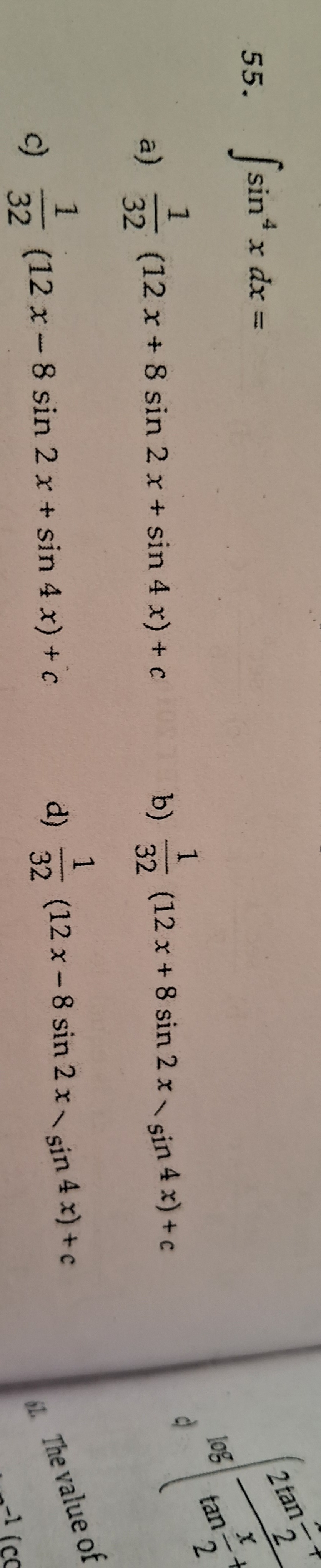
• A. $\frac{1}{32}(12x + 8sin2x + sin4x) + c$
• B. $\frac{1}{32}(12x + 8sin2x \sin^4 x) + c$
• C. $\frac{1}{32}(12x - 8sin2x + sin4x) + c$
• D. $\frac{1}{32}(12x - 8sin2x \sin^4 x) + c$

Answer 1

Answer: (C)

$\frac{1}{32}(12x - 8\sin2x + \sin4x) + C$

Answer 2

We start with the power reduction formula:

$$\sin^4 x = \frac{3}{8} - \frac{1}{2}\cos2x + \frac{1}{8}\cos4x.$$

Integrate term-by-term:

$$\int \sin^4 x \, dx = \int \left(\frac{3}{8} - \frac{1}{2}\cos2x + \frac{1}{8}\cos4x\right) dx.$$ $$= \frac{3}{8}x - \frac{1}{2}\cdot\frac{\sin2x}{2} + \frac{1}{8}\cdot\frac{\sin4x}{4} + C.$$ $$= \frac{3}{8}x - \frac{\sin2x}{4} + \frac{\sin4x}{32} + C.$$

Expressing with denominator 32:

$$= \frac{12x - 8\sin2x + \sin4x}{32} + C.$$

Thus, the correct answer is Option (c).