Question
Question: If two equal vectors $\overline{A}$ and $\overline{B}$ are inclined at an angle $\theta$ and each of...
If two equal vectors A and B are inclined at an angle θ and each of magnitude is f, then ∣A−B∣
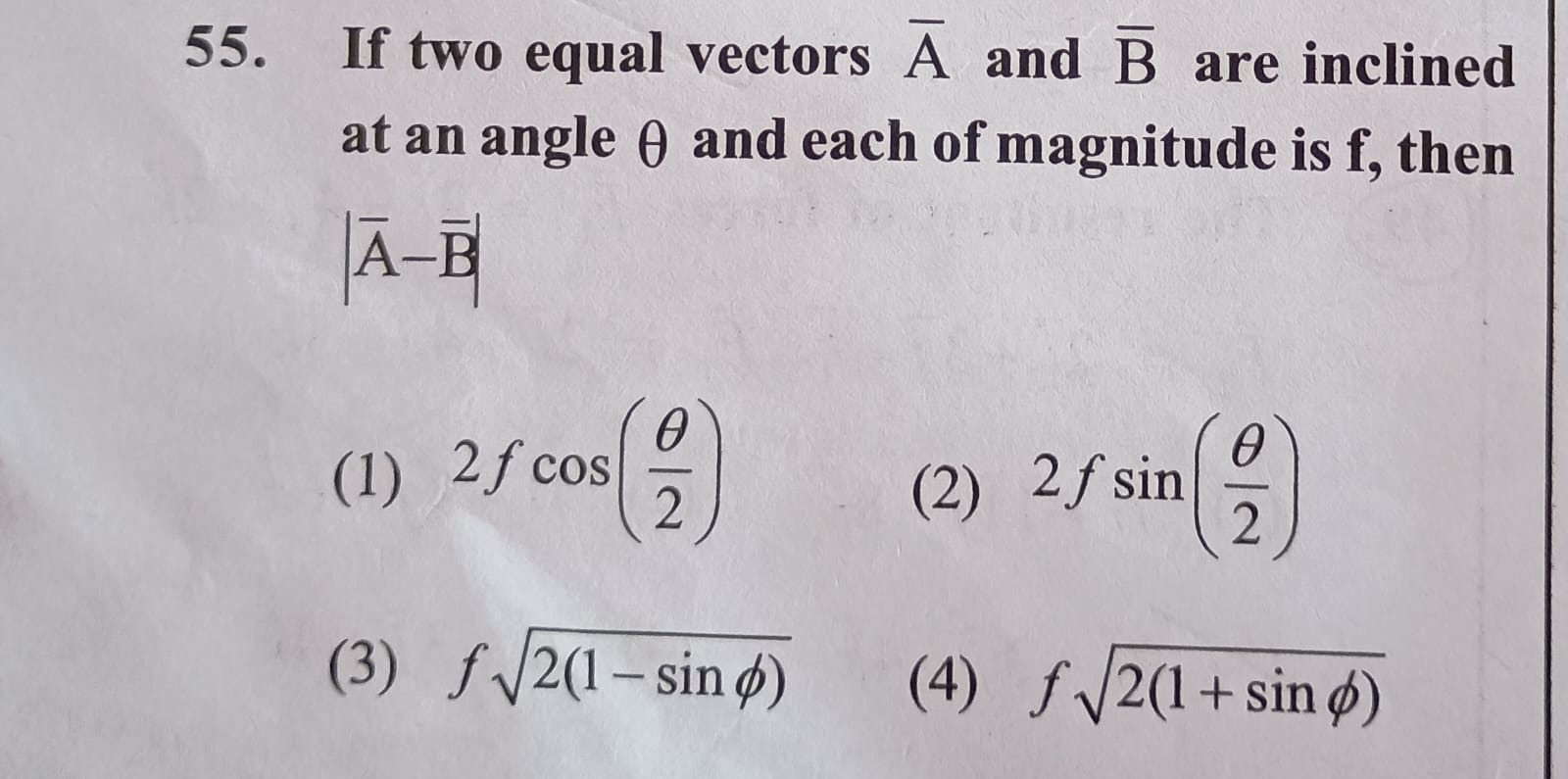
2fcos(2θ)
2fsin(2θ)
f2(1−sinϕ)
f2(1+sinϕ)
2fsin(2θ)
Solution
Let the two equal vectors be A and B. The magnitude of each vector is given as f, so ∣A∣=f and ∣B∣=f. The angle between the two vectors is θ. We need to find the magnitude of the difference between the two vectors, ∣A−B∣.
The magnitude of the difference of two vectors A and B is given by the formula: ∣A−B∣=∣A∣2+∣B∣2−2∣A∣∣B∣cosθ
Substitute the given magnitudes ∣A∣=f and ∣B∣=f into the formula: ∣A−B∣=f2+f2−2(f)(f)cosθ ∣A−B∣=2f2−2f2cosθ
Factor out 2f2 from the terms under the square root: ∣A−B∣=2f2(1−cosθ)
Now, use the trigonometric identity 1−cosθ=2sin2(2θ). Substitute this identity into the expression: ∣A−B∣=2f2(2sin2(2θ)) ∣A−B∣=4f2sin2(2θ)
Taking the square root, we get: ∣A−B∣=(2fsin(2θ))2 ∣A−B∣=∣2fsin(2θ)∣
Since f is a magnitude, f≥0. The angle θ between two vectors is typically considered in the range 0≤θ≤π. For this range, 0≤2θ≤2π, and sin(2θ)≥0. Therefore, ∣sin(2θ)∣=sin(2θ).
So, the magnitude of the difference is: ∣A−B∣=2fsin(2θ)
