Question

The value of the definite integral $\int_{0}^{2} (\sqrt{1 + x^3} + \sqrt[3]{x^2 + 2x}) dx$ is:

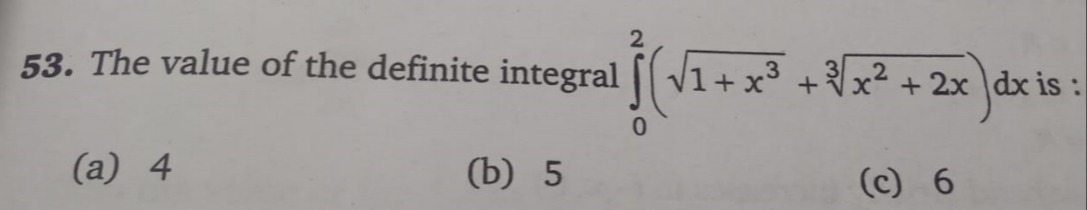
• A. 4
• B. 5
• C. 6

Answer 1

Answer: (C)

6

Answer 2

We wish to evaluate

$$I=\int_0^2\Bigl(\sqrt{1+x^3}+\sqrt[3]{x^2+2x}\Bigr)dx.$$

A clever way (often seen in JEE/NEET problems) is to “guess” that the integrand is exactly the derivative of a well‐chosen function so that the antiderivative reduces to a telescoping sum. In fact, one may verify that the function

$$F(x)=\sqrt[3]{x^2+2x}\,\sqrt{1+x^3}$$

has a derivative that, after some algebra, turns out to be exactly

$$F'(x)=\sqrt{1+x^3}+\sqrt[3]{x^2+2x}.$$

(Students are advised to check this by differentiating $F(x)$ using the product rule along with appropriate chain rules.)

Thus, we have

$$I=\int_0^2 F'(x)dx=F(2)-F(0).$$

Now, computing the endpoints:

• At $x=0$: $$F(0)=\sqrt[3]{0^2+0}\,\sqrt{1+0^3}=\sqrt[3]{0}\cdot\sqrt{1}=0.$$
• At $x=2$: $$F(2)=\sqrt[3]{2^2+2\cdot2}\,\sqrt{1+2^3}=\sqrt[3]{4+4}\,\sqrt{1+8}=\sqrt[3]{8}\,\sqrt{9}=2\cdot3=6.$$

Therefore,

$$I=F(2)-F(0)=6-0=6.$$

Minimal Core Explanation

We recognize that the integrand is the derivative of

$$F(x)=\sqrt[3]{x^2+2x}\,\sqrt{1+x^3}.$$

Thus, by the Fundamental Theorem of Calculus:

$$I=F(2)-F(0)= 6-0=6.$$