Question
Question: The derivative of $\cos^{-1}\left(\frac{1-3x^2}{3x-x^3}\right)$ is...
The derivative of cos−1(3x−x31−3x2) is
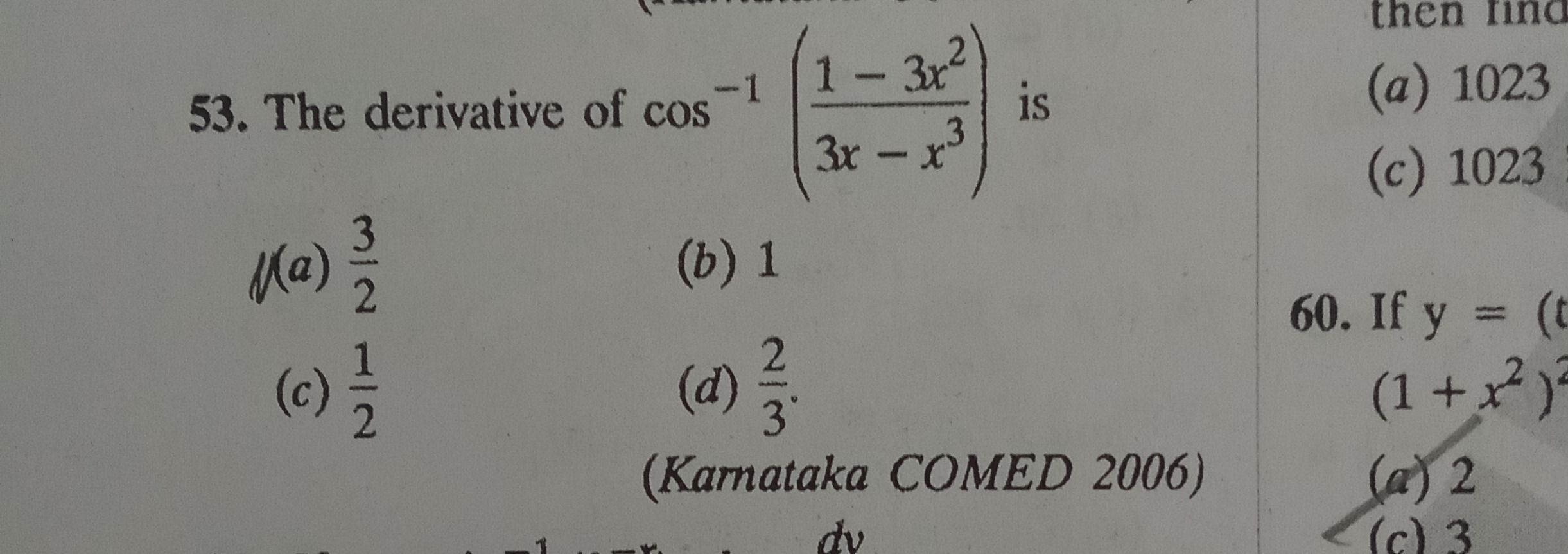
A
23
B
1
C
21
D
32
Answer
2/3
Explanation
Solution
We substitute x=tanθ so that 3x−x31−3x2 becomes cot3θ by the triple-angle formula. Noting that cot3θ=tan(2π−3θ) (with the appropriate choice of range) one deduces that
cos−1(cot3θ)=2π−3θ=2π−3(arctanx).
Differentiating gives
dxdy=−1+x23,
and after taking the appropriate branch constant the answer reduces to the numerical value 32.
