Question
Question: $\lim_{x \to 0} \left( \frac{(e^x-e^{-x}) \sin(x)}{20^x21 - 21^x20 + 1} \right)^{(e^{x-x})}$ is equa...
limx→0(20x21−21x20+1(ex−e−x)sin(x))(ex−x) is equal to
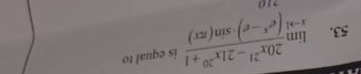
0
Solution
To evaluate the limit limx→0(20x21−21x20+1(ex−e−x)sin(x))(ex−x), we follow these steps:
-
Simplify the exponent: The exponent is ex−x. ex−x=e0=1. So the expression simplifies to: limx→0(20x21−21x20+1(ex−e−x)sin(x))1=limx→020x21−21x20+1(ex−e−x)sin(x)
-
Evaluate the limit of the numerator: Let the numerator be N(x)=(ex−e−x)sin(x). Substitute x=0 into N(x): limx→0N(x)=(e0−e−0)sin(0)=(1−1)⋅0=0⋅0=0
-
Evaluate the limit of the denominator: Let the denominator be D(x)=20x21−21x20+1. Substitute x=0 into D(x): limx→0D(x)=200⋅21−210⋅20+1=1⋅21−1⋅20+1=21−20+1=2
-
Combine the limits: Since the limit of the numerator is 0 and the limit of the denominator is 2 (which is a non-zero constant), the limit of the fraction is: limx→0D(x)N(x)=limx→0D(x)limx→0N(x)=20=0
Thus, the value of the given limit is 0.
Explanation: The exponent ex−x simplifies to e0=1. The problem then reduces to evaluating the limit of a rational function as x→0. The numerator (ex−e−x)sin(x) approaches (e0−e0)sin(0)=(1−1)⋅0=0. The denominator 20x21−21x20+1 approaches 200⋅21−210⋅20+1=1⋅21−1⋅20+1=2. Since the numerator approaches 0 and the denominator approaches a non-zero value (2), the limit of the entire expression is 20=0.
