Question
Question: Let a, b, c, d > 0 and $x = \frac{a}{a+b+d} + \frac{b}{a+b+c} + \frac{c}{b+c+d} + \frac{d}{a+c+d}$, ...
Let a, b, c, d > 0 and x=a+b+da+a+b+cb+b+c+dc+a+c+dd, then for some a,b,c,d the value of
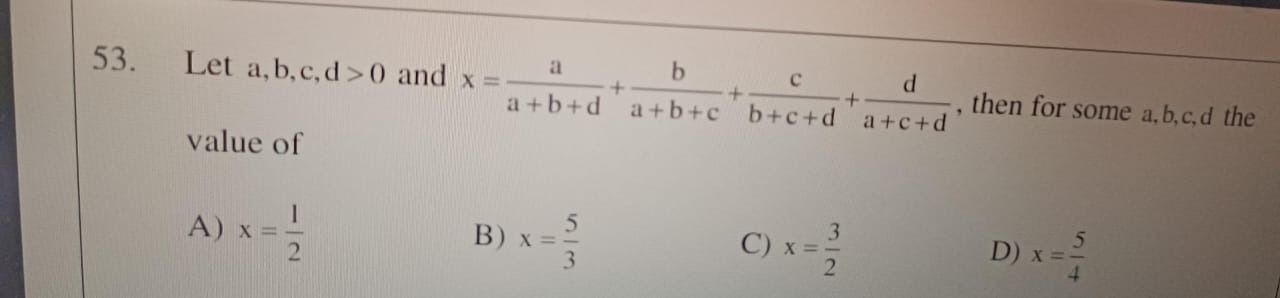
x=21
x=35
x=23
x=45
3/2
Solution
The expression for x is given by x=a+b+da+a+b+cb+b+c+dc+a+c+dd.
For any positive values of a, b, c, d, each term is positive and less than 1. Summing these gives 0<x<4.
By comparing each term with sum_of_all_variablesvariable, we showed that x>1.
By comparing each term with sum_of_two_variablesvariable, we showed that x<2.
So, for any positive a, b, c, d, the value of x is strictly between 1 and 2.
We check the given options. Options B, C, and D are in the range (1, 2). Option A is not.
We try to find if any of the values in B, C, D can be achieved.
Consider the case where a=c and b=d. The expression simplifies to x=a+2b2a+2a+b2b.
We set x=3/2 and a=1. This led to a quadratic equation for b, 2b2−7b+2=0. The roots are b=47±33, which are positive real numbers.
Thus, for a=c=1 and b=d=47+33 (or b=d=47−33), the value of x is 3/2.
Since we found positive values for a, b, c, d for which x=3/2, this is a possible value.
