Question
Question: $\underset{y\to\infty}{Lt} \frac{\sqrt{1+\sqrt{1+y^4}}-\sqrt{2}}{y^4}=$...
y→∞Lty41+1+y4−2=
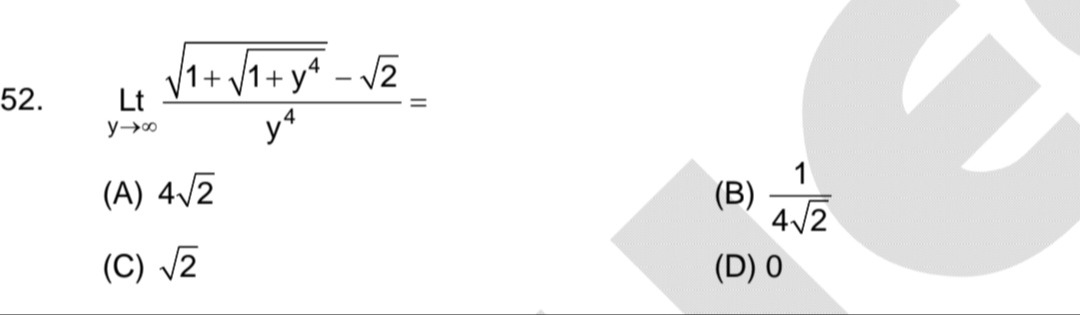
A
42
B
421
C
2
D
0
Answer
0
Explanation
Solution
Let x=y4. As y→∞, x→∞. The limit becomes x→∞Ltx1+1+x−2. Using rationalization: x→∞Ltx(1+1+x+2)(1+1+x−2)(1+1+x+2) =x→∞Ltx(1+1+x+2)1+1+x−2 =x→∞Ltx(1+1+x+2)1+x−1 For large x, 1+x≈x and 1+1+x≈x=x1/4. The expression becomes approximately x→∞Ltx(x1/4+2)x≈x→∞Ltx5/4x1/2=x→∞Ltx−3/4=0.
