Question

|\overline{A}+\overline{B}|=|\overline{A}-\overline{B}|$then the angle between$\overline{A}, \overline{B}$ is

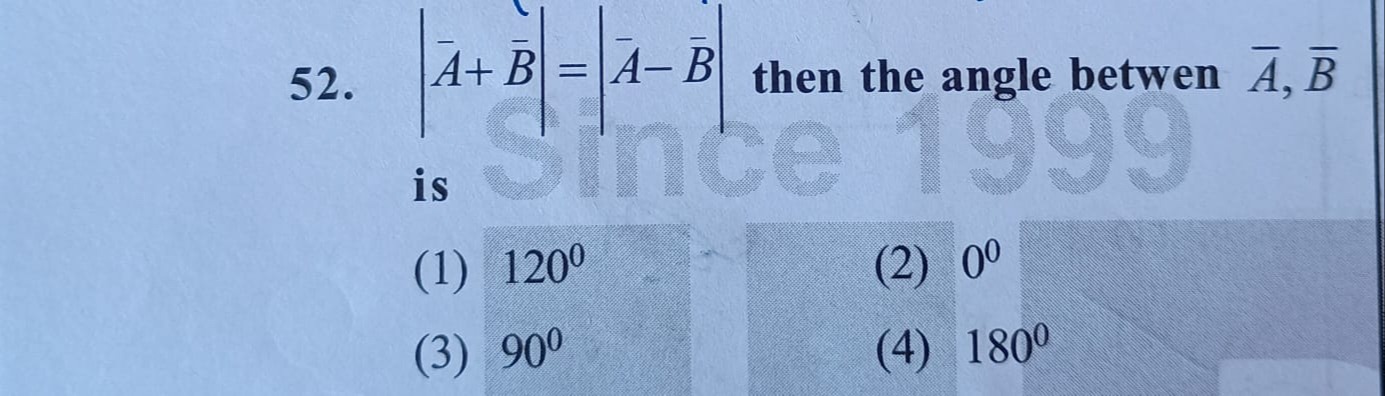
• A. $120^0$
• B. $0^0$
• C. $90^0$
• D. $180^0$

Answer 1

Answer: (C)

90 degrees

Answer 2

Given the condition $|\overline{A}+\overline{B}|=|\overline{A}-\overline{B}|$. Let $\theta$ be the angle between vectors $\overline{A}$ and $\overline{B}$.

The magnitude of the sum of two vectors is given by $|\overline{A}+\overline{B}| = \sqrt{|\overline{A}|^2 + |\overline{B}|^2 + 2|\overline{A}||\overline{B}|\cos\theta}$.

The magnitude of the difference of two vectors is given by $|\overline{A}-\overline{B}| = \sqrt{|\overline{A}|^2 + |\overline{B}|^2 - 2|\overline{A}||\overline{B}|\cos\theta}$.

The given condition is $|\overline{A}+\overline{B}|=|\overline{A}-\overline{B}|$. Squaring both sides, we get: $|\overline{A}+\overline{B}|^2=|\overline{A}-\overline{B}|^2$

Substitute the formulas for the squared magnitudes: $|\overline{A}|^2 + |\overline{B}|^2 + 2|\overline{A}||\overline{B}|\cos\theta = |\overline{A}|^2 + |\overline{B}|^2 - 2|\overline{A}||\overline{B}|\cos\theta$

Let $A = |\overline{A}|$ and $B = |\overline{B}|$. $A^2 + B^2 + 2AB\cos\theta = A^2 + B^2 - 2AB\cos\theta$

Subtract $A^2 + B^2$ from both sides: $2AB\cos\theta = -2AB\cos\theta$

Add $2AB\cos\theta$ to both sides: $2AB\cos\theta + 2AB\cos\theta = 0$ $4AB\cos\theta = 0$

This equation must hold. Assuming that $\overline{A}$ and $\overline{B}$ are non-null vectors, their magnitudes $A$ and $B$ are non-zero ($A \neq 0$ and $B \neq 0$). In this case, we can divide both sides by $4AB$: $\cos\theta = 0$

The angle $\theta$ between two vectors is conventionally taken to be in the range $[0^\circ, 180^\circ]$. The value of $\theta$ in this range for which $\cos\theta = 0$ is $\theta = 90^\circ$.