Question

Let $A=[a_{ij}]_{n \times n}$ such that $a_{ij}=\frac{(-1)^i(2i^2+1)}{4j^4+1}$, then value of $1+\lim_{n \to \infty}$(trace A) is

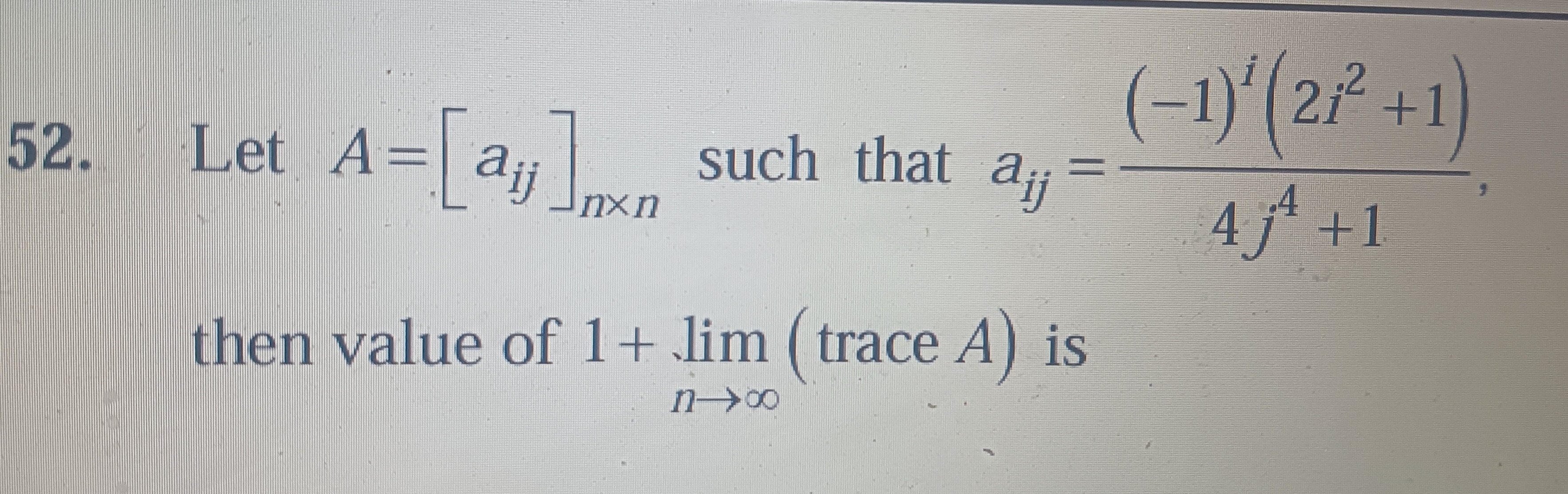
• A. 1/2
• B. -1/2
• C. 1
• D. 0

Answer 1

Answer: (A)

1/2

Answer 2

The trace of matrix $A$ is the sum of its diagonal elements $a_{ii}$. We need to find $\lim_{n \to \infty} \sum_{i=1}^n a_{ii}$, where $a_{ii} = \frac{(-1)^i(2i^2+1)}{4i^4+1}$. The fraction $\frac{2i^2+1}{4i^4+1}$ can be decomposed as $\frac{1}{2}\left(\frac{1}{2i^2-2i+1} + \frac{1}{2i^2+2i+1}\right)$. Let $f(i) = \frac{1}{2i^2-2i+1}$. Then $f(i+1) = \frac{1}{2i^2+2i+1}$. So, $a_{ii} = \frac{(-1)^i}{2}(f(i) + f(i+1))$. The sum $\sum_{i=1}^{\infty} a_{ii} = \frac{1}{2} \sum_{i=1}^{\infty} (-1)^i(f(i) + f(i+1))$. The partial sum $S_n = \frac{1}{2} \sum_{i=1}^n (-1)^i(f(i) + f(i+1))$ telescopes to $\frac{1}{2}(-f(1) + (-1)^n f(n+1))$. As $n \to \infty$, $f(n+1) \to 0$, so $\lim_{n \to \infty} S_n = \frac{1}{2}(-f(1))$. $f(1) = \frac{1}{2(1)^2-2(1)+1} = 1$. Thus, $\lim_{n \to \infty} (\text{trace } A) = \frac{1}{2}(-1) = -\frac{1}{2}$. The required value is $1 + \lim_{n \to \infty} (\text{trace } A) = 1 - \frac{1}{2} = \frac{1}{2}$.