Question
Question: If $f(x+1)=(-1)^{n+1}x-2f(x)$ for $x \in N$ and $f(1)=f(1986)$, Then sum of digits of $(f(1)+f(2)+.....
If f(x+1)=(−1)n+1x−2f(x) for x∈N and f(1)=f(1986), Then sum of digits of (f(1)+f(2)+...+f(1985)) is
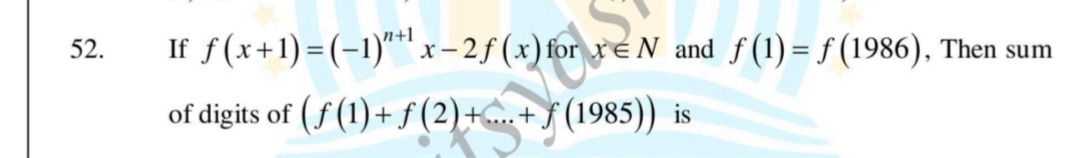
26
7
18
20
26
Solution
Let the given functional equation be f(x+1)=C⋅x−2f(x), where C=(−1)n+1 is a constant. We are given f(1)=f(1986). We need to find the sum of digits of S=∑x=11985f(x).
Summing the functional equation from x=1 to 1985: ∑x=11985f(x+1)+2∑x=11985f(x)=∑x=11985C⋅x The first term is ∑x=11985f(x+1)=f(2)+f(3)+⋯+f(1986). This can be written as (f(1)+f(2)+⋯+f(1985)+f(1986))−f(1)=S+f(1986)−f(1). The equation becomes: (S+f(1986)−f(1))+2S=C∑x=11985x Given f(1)=f(1986), the term f(1986)−f(1)=0. So, the equation simplifies to: 3S=C∑x=11985x The sum of the first 1985 natural numbers is 21985⋅(1985+1)=21985⋅1986=1985⋅993. 3S=C⋅(1985⋅993) S=C⋅31985⋅993 S=C⋅(1985⋅331) Calculating 1985⋅331: 1985×331=657035. So, S=C⋅657035.
Since C=(−1)n+1, C can be either 1 or −1. If C=1, then S=657035. The sum of digits is 6+5+7+0+3+5=26. If C=−1, then S=−657035. The sum of digits of a negative number is usually taken for its absolute value. The sum of digits of ∣S∣=657035 is 6+5+7+0+3+5=26.
In either case, the sum of digits is 26.
The final answer is 26.
