Question

At what temperature (in °C), the graph between $\left(\frac{1}{du} \cdot \frac{dN}{N}\right)$ (Y-axis) and u (X-axis) will be maximum at 200 ms⁻¹ for a sample of ideal gas (molar mass = 41.57 gm mol⁻¹)?

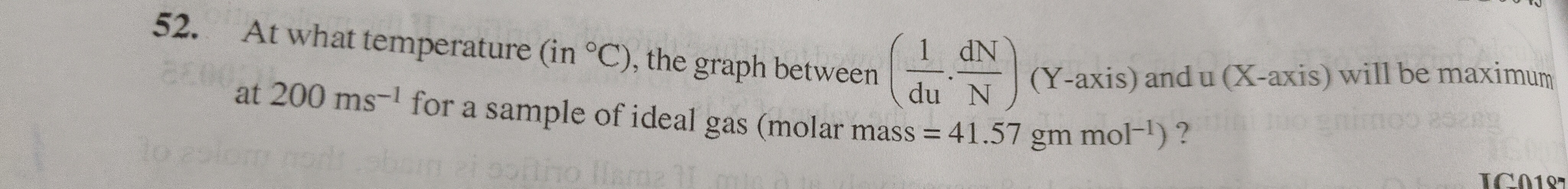
Answer 1

-173.15 °C

Answer 2

The term $\left(\frac{1}{du} \cdot \frac{dN}{N}\right)$ represents the Maxwell-Boltzmann distribution function for molecular speeds. The peak of this distribution occurs at the most probable speed ($u_{mp}$). We are given $u_{mp} = 200 \text{ ms}^{-1}$. The formula for the most probable speed is $u_{mp} = \sqrt{\frac{2RT}{M}}$. Rearranging for temperature $T$: $T = \frac{M u_{mp}^2}{2R}$. Given: $M = 41.57 \text{ gm mol}^{-1} = 41.57 \times 10^{-3} \text{ kg mol}^{-1}$, $u_{mp} = 200 \text{ ms}^{-1}$, $R = 8.314 \text{ J mol}^{-1} \text{ K}^{-1}$. $T = \frac{(41.57 \times 10^{-3}) \times (200)^2}{2 \times 8.314} \approx 100 \text{ K}$. Converting to °C: $T(\text{°C}) = 100 - 273.15 = -173.15 \text{ °C}$.