Question

If the length of an open organ pipe is 33.3 cm, then the frequency of fifth overtone will be ($V_{\text{sound}}$ = 333 m/s)

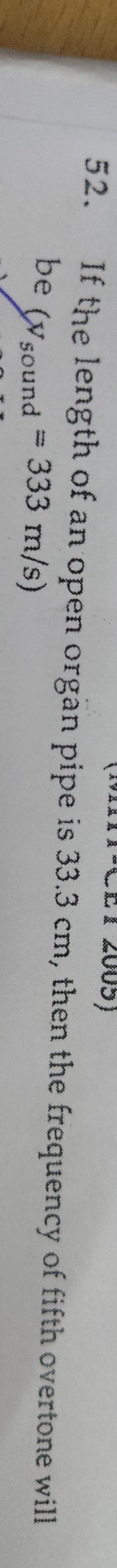
Answer 1

3000 Hz

Answer 2

For an open organ pipe, the resonant frequencies are given by:

$$f_n = n\left(\frac{v}{2L}\right)$$

where $n = 1, 2, 3, \dots$

The term "fifth overtone" means the sixth harmonic (since the first overtone corresponds to $n=2$). So, $n = 6$.

Given:

$$L = 33.3\, \text{cm} = 0.333\, \text{m}, \quad v = 333\, \text{m/s}$$

Now, substituting the values:

$$f_6 = 6\left(\frac{333}{2 \times 0.333}\right) = 6\left(\frac{333}{0.666}\right) = 6 \times 500 = 3000\, \text{Hz}$$