Question

The value of determining

$$\begin{vmatrix} \cos (\theta + \phi) & -\sin (\theta + \phi) & \cos 2\phi \\ \sin \theta & \cos \theta & \sin \phi \\ -\cos \theta & \sin \theta & \cos \phi \end{vmatrix}$$

is:

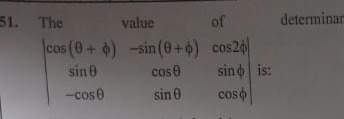
Answer 1

$1 + \cos 2\phi$

Answer 2

We expand the determinant along the first row: $D = \cos (\theta + \phi) \begin{vmatrix} \cos \theta & \sin \phi \\ \sin \theta & \cos \phi \end{vmatrix} - (-\sin (\theta + \phi)) \begin{vmatrix} \sin \theta & \sin \phi \\ -\cos \theta & \cos \phi \end{vmatrix} + \cos 2\phi \begin{vmatrix} \sin \theta & \cos \theta \\ -\cos \theta & \sin \theta \end{vmatrix}$

Evaluating the 2x2 determinants:

1. $\begin{vmatrix} \cos \theta & \sin \phi \\ \sin \theta & \cos \phi \end{vmatrix} = (\cos \theta)(\cos \phi) - (\sin \phi)(\sin \theta) = \cos(\theta + \phi)$
2. $\begin{vmatrix} \sin \theta & \sin \phi \\ -\cos \theta & \cos \phi \end{vmatrix} = (\sin \theta)(\cos \phi) - (\sin \phi)(-\cos \theta) = \sin \theta \cos \phi + \cos \theta \sin \phi = \sin(\theta + \phi)$
3. $\begin{vmatrix} \sin \theta & \cos \theta \\ -\cos \theta & \sin \theta \end{vmatrix} = (\sin \theta)(\sin \theta) - (\cos \theta)(-\cos \theta) = \sin^2 \theta + \cos^2 \theta = 1$

Substituting these values back: $D = \cos (\theta + \phi) [\cos(\theta + \phi)] + \sin (\theta + \phi) [\sin(\theta + \phi)] + \cos 2\phi [1]$ $D = \cos^2 (\theta + \phi) + \sin^2 (\theta + \phi) + \cos 2\phi$ Using the identity $\cos^2 x + \sin^2 x = 1$: $D = 1 + \cos 2\phi$ This can also be written as $2\cos^2 \phi$.