Question

The top in the figure has a moment of inertia equal to $4.0 \times 10^{-4} kg m^2$ and is initially at rest. It is free to rotate about the stationary axis AA'. A string wrapped around a peg along the axis of the top is pulled in such a manner as to maintain a constant tension of 5.57 N. If the string does not slip while it is unwound from the peg, what is the angular speed of the top after 80.0cm of string has been pulled off the peg.

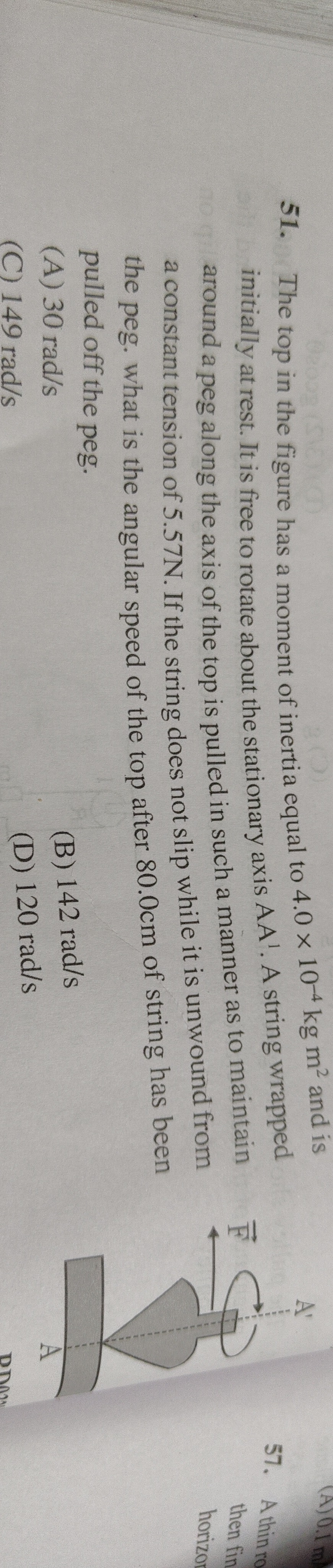
• A. 30 rad/s
• B. 149 rad/s
• C. 142 rad/s
• D. 120 rad/s

Answer 1

Answer: (B)

149 rad/s

Answer 2

The problem can be solved using the work-energy theorem for rotational motion.

1. Identify Given Values:

   • Moment of inertia, $I = 4.0 \times 10^{-4} \text{ kg m}^2$
   • Initial angular speed, $ω_0 = 0 \text{ rad/s}$ (since it's initially at rest)
   • Constant tension, $T = 5.57 \text{ N}$
   • Length of string pulled off, $L = 80.0 \text{ cm} = 0.80 \text{ m}$

2. Calculate the Work Done by the Tension:

   The work done by the constant tension force as the string is pulled off is given by:

   $W = T \times L$

   $W = 5.57 \text{ N} \times 0.80 \text{ m}$

   $W = 4.456 \text{ J}$

3. Apply the Work-Energy Theorem:

   According to the work-energy theorem, the work done on the top is converted into its rotational kinetic energy.

   $W = \Delta KE_{rot}$

   Since the top starts from rest, the initial rotational kinetic energy is zero ($KE_{initial} = 0$).

   So, $W = KE_{final}$

   The rotational kinetic energy is given by $KE_{rot} = \frac{1}{2} I ω^2$.

   Therefore, $W = \frac{1}{2} I ω^2$

4. Solve for the Final Angular Speed (ω):

   Substitute the values into the equation:

   $4.456 = \frac{1}{2} \times (4.0 \times 10^{-4}) \times ω^2$

   $4.456 = (2.0 \times 10^{-4}) \times ω^2$

   $ω^2 = \frac{4.456}{2.0 \times 10^{-4}}$

   $ω^2 = 2.228 \times 10^4$

   $ω^2 = 22280$

   $ω = \sqrt{22280}$

   $ω \approx 149.26 \text{ rad/s}$

5. Compare with Options:

   The calculated angular speed $149.26 \text{ rad/s}$ is closest to $149 \text{ rad/s}$.

The final answer is $\boxed{\text{149 rad/s}}$.

Explanation:

The work done by the constant tension on the string is calculated as $W = \text{Tension} \times \text{Length}$. This work is entirely converted into the rotational kinetic energy of the top, as it starts from rest. The rotational kinetic energy is given by $KE_{rot} = \frac{1}{2} I ω^2$. Equating the work done to the final rotational kinetic energy allows us to solve for the final angular speed $ω$.