Solveeit Logo
Login

Question

Question: Let $I = \int_{0}^{2} [|x^{2} - 5x + 4| + [\sin \frac{3\pi}{2}x]] dx$; (where [.] represents greates...

Let I=∫02[∣x2−5x+4∣+[sin⁡3π2x]]dxI = \int_{0}^{2} [|x^{2} - 5x + 4| + [\sin \frac{3\pi}{2}x]] dx; (where [.] represents greatest integer function) then I+2/3I + 2/3 is

A

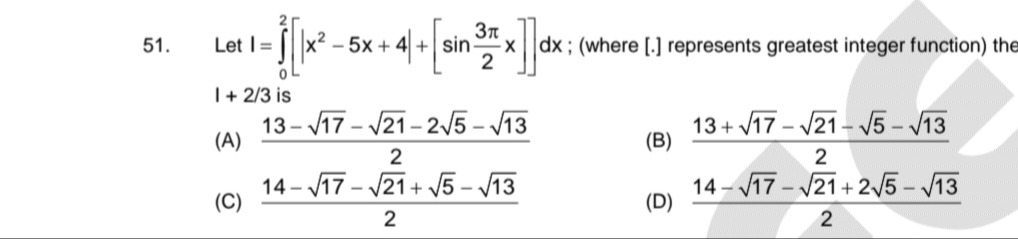
13−17−21−25−132\frac{13 - \sqrt{17} - \sqrt{21} - 2\sqrt{5} - \sqrt{13}}{2}

B

13+17−21−5−132\frac{13 + \sqrt{17} - \sqrt{21} - \sqrt{5} - \sqrt{13}}{2}

C

14−17−21+5−132\frac{14 - \sqrt{17} - \sqrt{21} + \sqrt{5} - \sqrt{13}}{2}

D

14−17−21+25−132\frac{14 - \sqrt{17} - \sqrt{21} + 2\sqrt{5} - \sqrt{13}}{2}

Answer

The provided options do not match the calculated answer.

Explanation

Solution

The integral is I=∫02[∣x2−5x+4∣+[sin⁡3π2x]]dxI = \int_{0}^{2} [|x^{2} - 5x + 4| + [\sin \frac{3\pi}{2}x]] dx.

  1. Analyze ∣x2−5x+4∣|x^2 - 5x + 4|: The roots of x2−5x+4=0x^2 - 5x + 4 = 0 are x=1x=1 and x=4x=4. For x∈[0,1]x \in [0, 1], x2−5x+4≥0x^2 - 5x + 4 \ge 0, so ∣x2−5x+4∣=x2−5x+4|x^2 - 5x + 4| = x^2 - 5x + 4. For x∈(1,2]x \in (1, 2], x2−5x+4<0x^2 - 5x + 4 < 0, so ∣x2−5x+4∣=−(x2−5x+4)=−x2+5x−4|x^2 - 5x + 4| = -(x^2 - 5x + 4) = -x^2 + 5x - 4.

  2. Analyze [sin⁡3π2x][\sin \frac{3\pi}{2}x]: The period of sin⁡3π2x\sin \frac{3\pi}{2}x is T=2π3π/2=43T = \frac{2\pi}{3\pi/2} = \frac{4}{3}.

    • For x∈[0,2/3)x \in [0, 2/3), 3π2x∈[0,π)\frac{3\pi}{2}x \in [0, \pi), so sin⁡(3π2x)∈[0,1)\sin(\frac{3\pi}{2}x) \in [0, 1), which means [sin⁡3π2x]=0[\sin \frac{3\pi}{2}x] = 0.
    • For x∈[2/3,4/3)x \in [2/3, 4/3), 3π2x∈[π,2π)\frac{3\pi}{2}x \in [\pi, 2\pi), so sin⁡(3π2x)∈[−1,0)\sin(\frac{3\pi}{2}x) \in [-1, 0), which means [sin⁡3π2x]=−1[\sin \frac{3\pi}{2}x] = -1.
    • For x∈[4/3,2]x \in [4/3, 2], 3π2x∈[2π,3π]\frac{3\pi}{2}x \in [2\pi, 3\pi]. sin⁡(3π2x)\sin(\frac{3\pi}{2}x) ranges from 00 to 11. For integration purposes, we consider [sin⁡3π2x]=0[\sin \frac{3\pi}{2}x] = 0 since the value is 1 only at a single point (x=5/3x=5/3).

  3. Evaluate the integral by splitting intervals:

    • ∫02/3(x2−5x+4+0)dx=[x33−5x22+4x]02/3=13481\int_{0}^{2/3} (x^2 - 5x + 4 + 0) dx = [\frac{x^3}{3} - \frac{5x^2}{2} + 4x]_{0}^{2/3} = \frac{134}{81}.
    • ∫2/31(x2−5x+4−1)dx=∫2/31(x2−5x+3)dx=[x33−5x22+3x]2/31=−25162\int_{2/3}^{1} (x^2 - 5x + 4 - 1) dx = \int_{2/3}^{1} (x^2 - 5x + 3) dx = [\frac{x^3}{3} - \frac{5x^2}{2} + 3x]_{2/3}^{1} = -\frac{25}{162}.
    • ∫14/3(−x2+5x−4−1)dx=∫14/3(−x2+5x−5)dx=[−x33+5x22−5x]14/3=−29162\int_{1}^{4/3} (-x^2 + 5x - 4 - 1) dx = \int_{1}^{4/3} (-x^2 + 5x - 5) dx = [-\frac{x^3}{3} + \frac{5x^2}{2} - 5x]_{1}^{4/3} = -\frac{29}{162}.
    • ∫4/32(−x2+5x−4+0)dx=[−x33+5x22−4x]4/32=8281\int_{4/3}^{2} (-x^2 + 5x - 4 + 0) dx = [-\frac{x^3}{3} + \frac{5x^2}{2} - 4x]_{4/3}^{2} = \frac{82}{81}.

  4. Sum the results: I=13481−25162−29162+8281=268−25−29+164162=378162=73I = \frac{134}{81} - \frac{25}{162} - \frac{29}{162} + \frac{82}{81} = \frac{268 - 25 - 29 + 164}{162} = \frac{378}{162} = \frac{7}{3}.

  5. Calculate I+2/3I + 2/3: I+23=73+23=93=3I + \frac{2}{3} = \frac{7}{3} + \frac{2}{3} = \frac{9}{3} = 3.

Since 3 is not among the options and the options contain square roots, there is likely an error in the question or the provided options. Based on the given integral, the correct value for I+2/3I + 2/3 is 3.