Question
Question: If $\alpha, \beta, \gamma \in [0, 2\pi]$ and $cos\alpha + cos\beta + cos\gamma = \frac{24}{17}$ and ...
If α,β,γ∈[0,2π] and cosα+cosβ+cosγ=1724 and sinα+sinβ+sinγ=1745, then value of cosγ+2cosβ+3cosαcosα+2cosβ+3cosγ+sinγ+2sinβ+3sinαsinα+2sinβ+3sinγ is
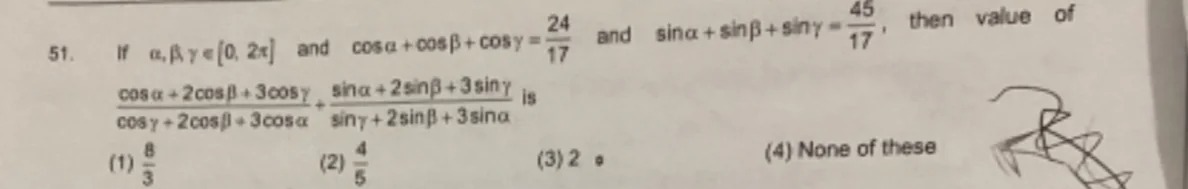
38
54
2
None of these
2
Solution
Let z1=cosα+isinα, z2=cosβ+isinβ, and z3=cosγ+isinγ. We are given: cosα+cosβ+cosγ=1724 sinα+sinβ+sinγ=1745
Let Z=z1+z2+z3. Z=(cosα+cosβ+cosγ)+i(sinα+sinβ+sinγ) Z=1724+i1745=1724+45i
The magnitude of Z is: ∣Z∣=1724+45i=171∣24+45i∣ ∣Z∣=171242+452=171576+2025=1712601 Since 512=2601, we have: ∣Z∣=1751=3
We also know that ∣z1∣=1, ∣z2∣=1, and ∣z3∣=1 because they are complex numbers on the unit circle (eiθ). By the triangle inequality for complex numbers, ∣z1+z2+z3∣≤∣z1∣+∣z2∣+∣z3∣. In our case, ∣Z∣=3 and ∣z1∣+∣z2∣+∣z3∣=1+1+1=3. The equality ∣z1+z2+z3∣=∣z1∣+∣z2∣+∣z3∣ holds if and only if z1,z2,z3 have the same argument, meaning they lie on the same ray from the origin. Since ∣z1∣=∣z2∣=∣z3∣=1, this implies z1=z2=z3.
eiα=eiβ=eiγ This implies α≡β(mod2π) and β≡γ(mod2π). Given that α,β,γ∈[0,2π], the only possibility is α=β=γ.
Let α=β=γ. Substituting this into the given equations: 3cosα=1724⟹cosα=178 3sinα=1745⟹sinα=1715 We can verify that cos2α+sin2α=(178)2+(1715)2=28964+225=289289=1, which is consistent.
Now we need to evaluate the given expression: E=cosγ+2cosβ+3cosαcosα+2cosβ+3cosγ+sinγ+2sinβ+3sinαsinα+2sinβ+3sinγ Since α=β=γ, let c=cosα=8/17 and s=sinα=15/17. The expression becomes: E=c+2c+3cc+2c+3c+s+2s+3ss+2s+3s E=6c6c+6s6s Since c=8/17=0 and s=15/17=0, the fractions are well-defined and simplify to: E=1+1=2
The value of the expression is 2.
