Solveeit Logo
Login

Question

Question: 500 ml of 0.2M aqueous solution of acetic acid is mixed with 500ml of 0.2M HCl at \[25^\circ C.\] ...

500 ml of 0.2M aqueous solution of acetic acid is mixed with 500ml of 0.2M HCl at 25∘C.25^\circ C.
(a) Calculate the degree of dissociation of acetic acid in the resulting solution and pH{pH} of the solution.
(b) If 6g of NaOH is added to the above solution, determine final pH{pH}. Assume there is no change in volume on mixing Ka for acetic acid is 1.75×10−5 ML−11.75 \times {10^{ - 5}}{\text{ M}}{{\text{L}}^{ - 1}}.

Explanation

Solution

The solution which resists a change in the pH value on the addition of a small amount of acid or base is called buffer solution. Most of the important buffer solutions generally consist of mixtures of weak acids and their salts or weak bases and their salts. These buffer solutions are known as acidic buffers and basic buffers.

Complete step by step answer:
First, we should know what is the degree of dissociation?
The phenomenon of generating the current carrying free ions that are dissociated from the fraction of solute at the given concentration is called the degree of dissociation.
a) When 500ml, 0.2M aqueous solution of acetic acid is mixed with 500ml, 0.2M HCl at 25∘C25^\circ C, the volume of solution is doubled, then the concentration of CH3COOHC{H_3}COOH and concentration of HCl is halved.
∴[CH3COOH]=0.22=0.1M\therefore \left[ {C{H_3}COOH} \right] = \dfrac{{0.2}}{2} = 0.1M
[HCl]=0.22=0.1M\left[ {HCl} \right] = \dfrac{{0.2}}{2} = 0.1M
To find the degree of dissociation of CH3COOHC{H_3}COOH

∵ after mixing the concentration of H+=0.1+Cα  \because {\text{ after mixing}} \\\ {\text{the concentration}} \\\ {\text{of }}{{\text{H}}^ + } = 0.1 + C\alpha \\\

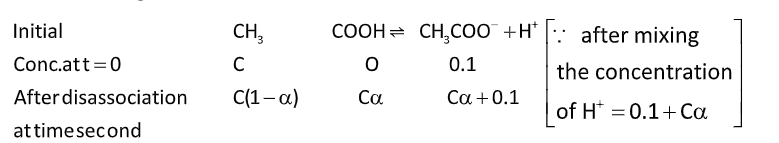
Ka=[CH3COO−][H+][CH3COOH]{K_a} = \dfrac{{\left[ {C{H_3}CO{O^ - }} \right]\left[ {{H^ + }} \right]}}{{\left[ {C{H_3}COOH} \right]}}
Ka=Cα×(0.1+Cα)C(1−α){K_a} = \dfrac{{C\alpha \times \left( {0.1 + C\alpha } \right)}}{{C\left( {1 - \alpha } \right)}}……... (i)
On approximation, α\alpha is very small, then CαC\alpha can be neglected then equation (i) becomes.

Ka=Cα×0.1C ∴1.75×10−5=0.1×α α=1.75×10−50.1 α=1.75×10−4  {K_a} = \dfrac{{C\alpha \times 0.1}}{C} \\\ \therefore 1.75 \times {10^{ - 5}} = 0.1 \times \alpha \\\ \alpha = \dfrac{{1.75 \times {{10}^{ - 5}}}}{{0.1}} \\\ \alpha = 1.75 \times {10^{ - 4}} \\\

[Given Ka=1.75×10−5ML−1]\left[ {Given{\text{ }}{{\text{K}}_a} = 1.75 \times {{10}^{ - 5}}M{L^{ - 1}}} \right]
The degree of dissociation of CH3COOH(α)=1.75×10−4C{H_3}COOH\left( \alpha \right) = 1.75 \times {10^{ - 4}}
Also, pH{pH} of the resulting solution.
[H+]=0.1+Cα=0.1[H^+]=0.1+C\alpha=0.1 [Because CαC\alpha can be neglected as α\alpha is very small]

Then pH=−log⁡[H+]{pH} = - \log \left[ {{H^ + }} \right]

= - \log \left( {0.1} \right) \\\ = - \log \left( {{{10}^{ - 1}}} \right) \\\ = - \left( { - 1} \right)\log 10 \\\ {pH} = 1 \\\ $$ $$\left[ {\because \log {\text{ 10 = 1}}} \right]$$ (b) To calculate the number of moles of NaOH, the formula is given below: moles of NaOH$$ = \dfrac{{Given{\text{ weight of NaOH}}}}{{Molar{\text{ mass of NaOH}}}}$$ Then number of moles of NaOH $$ = \dfrac{{\text{6}}}{{40}}$$ $$ = 0.15{\text{ }}moles.$$ Thus, milli moles of NaOH $$ = 0.15 \times 1000 = 150m{\text{ moles}}{\text{.}}$$ Molarity is defined as the moles or amount of the solute per unit volume of the solution. Also, m moles of $$C{H_3}COOH = 500 \times 0.2$$$$$$

moles = molarity \times vol. \\
\left( {\because vol.in{\text{ ml}}} \right) \\

$$ = 100ml.$$ First of all, when NaOH is added to a solution of $$C{H_3}COOH$$and HCl, first NaOH react with HCl and then react with $$C{H_3}COOH$$ $$\therefore \mathop {NaOH}\limits_{150} + \mathop {HCl}\limits_{100} \to NaCl + {H_2}O$$ Left moles of NaOH $$ = 150 - 100 = 50$$ To calculate $${pH}$$of the solution of weak acid $$\left( {C{H_3}COOH} \right)$$and strong base $$\left( {NaOH} \right).$$

{pH} = {p^{{K_a}}} + \log \dfrac{{\left[ {Salt} \right]}}{{\left[ {Acid} \right]}} \\
\Rightarrow {pH} = - \log {K_a} + \log \dfrac{{\left[ {Salt} \right]}}{{\left[ {Acid} \right]}} \\

Now, putting values in the above equation, $${pH} = - \log \left( {1.75 \times {{10}^{ - 5}} + \log \dfrac{{50}}{{50}}} \right)$$ Solving the above equation,

{pH} = - \log \left( {1.75 \times {{10}^{ - 5}}} \right) + 1{\text{ }}\left[ {\because \log {\text{1 = 0}}} \right] \\
\Rightarrow {pH} = - \log ,,1.{\text{75}} - \log {\text{ 1}}{{\text{0}}^{ - 5}} \\
\Rightarrow {pH} = - \log ,,1.75 - \left( { - 5} \right)\log ,,10 \\
\Rightarrow {pH} = - 0.24 + 5 \\
\therefore {pH} = 4.76 \\

∗∗Note:∗∗Italsogivesaninsighttotheeasewithwhichanatomcanchangeitselfintocationbylosingelectrons.IonizationenergyisexpressedinunitsofkJ/mol.Ionizationenergyisalwayspositive.Thetermionizationenergyisnotappropriateandistakenasthefirstionizationenergy,secondionizationenergy,thirdionizationenergyfortheenergychangesrequiredforremovaloffirst,second,thirdelectronrespectively. **Note:** It also gives an insight to the ease with which an atom can change itself into cation by losing electrons. Ionization energy is expressed in units of kJ/mol. Ionization energy is always positive. The term ionization energy is not appropriate and is taken as the first ionization energy, second ionization energy, third ionization energy for the energy changes required for removal of first, second, third electron respectively.