Question
Question: Let A be a symmetric matrix such that |A| = 2 and $A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} ...
Let A be a symmetric matrix such that |A| = 2 and A=[2112][33αβ]. If the sum of the diagonal
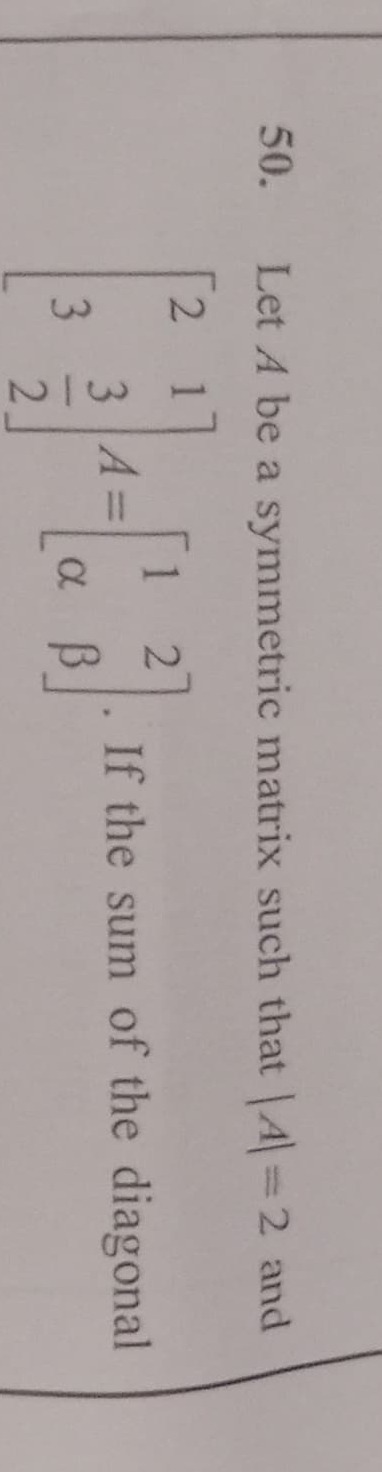
164/9
Solution
The problem statement is incomplete. It ends with "If the sum of the diagonal". Assuming the question asks for the sum of the diagonal elements of matrix A, we proceed as follows:
Let the given matrices be M1=[2112] and M2=[33αβ]. Matrix A is given by A=M1M2.
1. Calculate Matrix A: A=[2112][33αβ]=[(2)(3)+(1)(3)(1)(3)+(2)(3)(2)(α)+(1)(β)(1)(α)+(2)(β)] A=[6+33+62α+βα+2β]=[992α+βα+2β]
2. Use the condition that A is a symmetric matrix:
A matrix A=[aij] is symmetric if aij=aji for all i,j. For a 2x2 matrix, this means the off-diagonal elements must be equal. From matrix A, we have a12=2α+β and a21=9. Therefore, 2α+β=9. (Equation 1)
3. Use the condition that ∣A∣=2 (Determinant of A is 2):
The determinant of a 2x2 matrix [acbd] is ad−bc. ∣A∣=(9)(α+2β)−(2α+β)(9)=2 Factor out 9: 9[(α+2β)−(2α+β)]=2 9[α+2β−2α−β]=2 9[β−α]=2 β−α=92 This can be written as −α+β=92. (Equation 2)
4. Solve the system of linear equations for α and β:
We have two equations:
- 2α+β=9
- −α+β=92
Subtract Equation 2 from Equation 1: (2α+β)−(−α+β)=9−92 2α+β+α−β=981−2 3α=979 α=2779
Substitute the value of α back into Equation 1 to find β: 2(2779)+β=9 27158+β=9 β=9−27158 β=279×27−158 β=27243−158 β=2785
5. Calculate the sum of the diagonal elements of A:
The diagonal elements of A are a11=9 and a22=α+2β. Sum of diagonal elements = a11+a22=9+(α+2β) Substitute the values of α and β: Sum =9+(2779+2(2785)) Sum =9+(2779+27170) Sum =9+(2779+170) Sum =9+27249 Simplify the fraction 27249 by dividing the numerator and denominator by 3: 27÷3249÷3=983 Sum =9+983 Sum =99×9+83 Sum =981+83 Sum =9164
