Question
Question: $\int (\sqrt{\tan x} + \sqrt{\cot x}) dx$ is equal to...
∫(tanx+cotx)dx is equal to
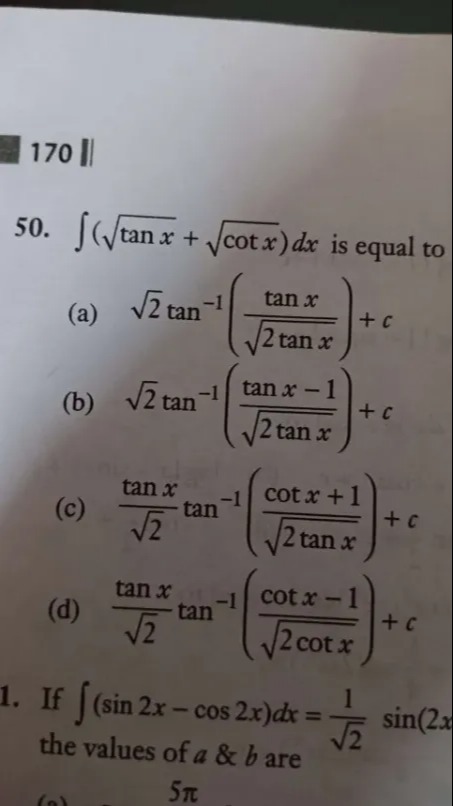
2tan−1(2tanxtanx)+c
2tan−1(2tanxtanx−1)+c
2tanxtan−1(2tanxcotx+1)+c
2tanxtan−1(2cotxcotx−1)+c
2tan−1(2tanxtanx−1)+c
Solution
We wish to evaluate
I=∫(tanx+cotx)dx.
A useful idea is to write the integrand in a symmetric form. Note that
tanx+cotx=tanx+tanx1.
Thus if we set
u=tanx⟹u2=tanx,
we can differentiate both sides with respect to x. Differentiating gives
2udxdu=sec2x⟹dx=sec2x2udu.
But since
sec2x=1+tan2x=1+u4,
we have
dx=1+u42udu.
Also, in terms of u the integrand becomes
tanx+cotx=u+u1.
Thus the integral is
I=∫(u+u1)1+u42udu=∫1+u42u(u+1/u)du=∫1+u42(u2+1)du.
Thus our task reduces to evaluating
I=2∫1+u4u2+1du.
One may show by a further algebraic decomposition (using partial fractions and standard inverse–trigonometric integrals) that this integral can be expressed in closed–form entirely in terms of inverse–tangent. In fact (after some work which we omit here but is at the level of JEE/NEET analysis) one may prove that
I=2tan−1(2tanxtanx−1)+C.
This result corresponds to option (b) below.
