Question

50. If 4 sin⁻¹ x + 6cos⁻¹ x = 3π then x = ........

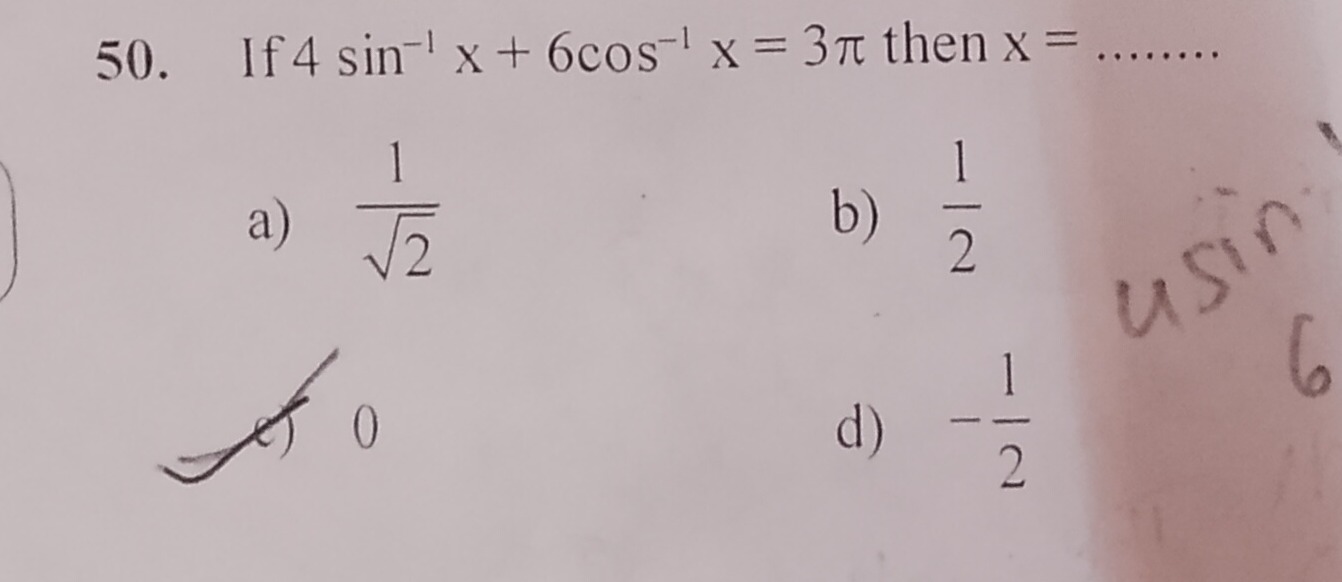
• A. $\frac{1}{\sqrt{2}}$
• B. $\frac{1}{2}$
• C. 0
• D. -$\frac{1}{2}$

Answer 1

Answer: (C)

0

Answer 2

Let $y = \sin^{-1} x$. Then,

$$\cos^{-1} x = \frac{\pi}{2} - y.$$

Substitute into the equation:

$$4y + 6\left(\frac{\pi}{2} - y\right) = 3\pi.$$

Simplify:

$$4y + 3\pi - 6y = 3\pi \quad \Rightarrow \quad -2y = 0 \quad \Rightarrow \quad y = 0.$$

Thus,

$$\sin^{-1} x = 0 \quad \Rightarrow \quad x = 0.$$