Question
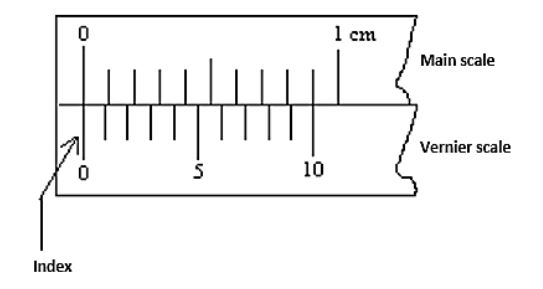
Question: 50 divisions on the Vernier scale is coinciding with 49 divisions on the main scale of a Vernier cal...
50 divisions on the Vernier scale is coinciding with 49 divisions on the main scale of a Vernier calliper. What is the least count of instruments, if graduation on the main scale is 2 mm?
A.251mmB.501mmC.492mmD.491mm
Solution
The smallest value that can be measured by a specific instrument is known as the least count. The measured and found values are accurate only up to this value. Least count of an instrument is given as the difference between main scale division and Vernier scale division. These may help us to solve this question.
Complete step-by-step answer:
It is already mentioned in the question that the main scale reading is 50 and Vernier scale division is 49.
So that we can write like this,
50VSD=49MSD
Therefore one Vernier scale division can be found using this,
1VSD=5049MSD
As we know that the least count of an instrument is given as the difference between main scale division and Vernier scale division.
It is mentioned in the question that,
MSD=2
Therefore we can write that,
L.C=MSD−VSD=2(1−5049)
Hence, the least count of a material is given as,
L.C=2(501)=251mm
So, the correct answer is “Option A”.
Note: One main scale division or 1MSD is referred to as the distance between the two successive marks on the main scale. One Vernier scale division or 1VSD is given as the distance between two successive marks on the Vernier scale. A Vernier scale has been used as a visual aid in order to make an accurate measurement of reading between two markings on a linear scale with the help of mechanical interpolation. This will help in increasing resolution and reducing measurement uncertainty by the use of Vernier scale in order to reduce human estimation error.
