Question
Question: $x \in \left[-\frac{2029\pi}{2}; -\frac{2027\pi}{2}\right]$...
x∈[−22029π;−22027π]
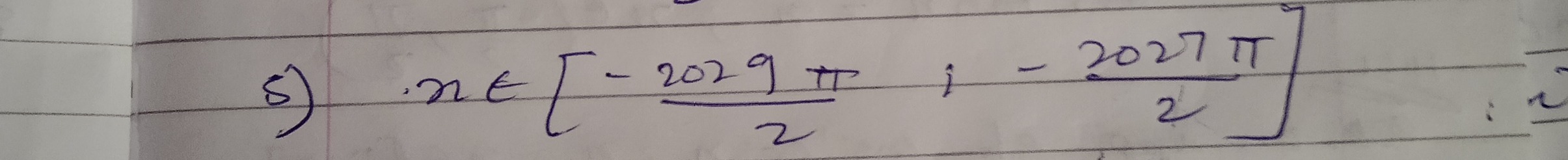
Answer
x+1014\pi
Explanation
Solution
For any x∈[nπ−2π,nπ+2π], we have:
sin−1(sinx)=(−1)n(x−nπ).For the interval
x∈[−22029π,−22027π],set
nπ−2π=−22029π⟹nπ=−22029π+2π=−22028π=−1014π.Thus, n=−1014 and consequently,
nπ+2π=−1014π+2π=−22027π.Since −1014 is even, (−1)n=(−1)−1014=1. Therefore:
sin−1(sinx)=x−(−1014π)=x+1014π.