Question

Two different composite numbers A and B are factorised as:

$A = (5^p \times 2^q)$ and $B = (3^p \times 2^q)$, where $p$ and $q$ are WHOLE numbers.

If $LCM$ of $A$ and $B$ always ends with 5 which of the following is the $HCF$ of $A$ and $B$?

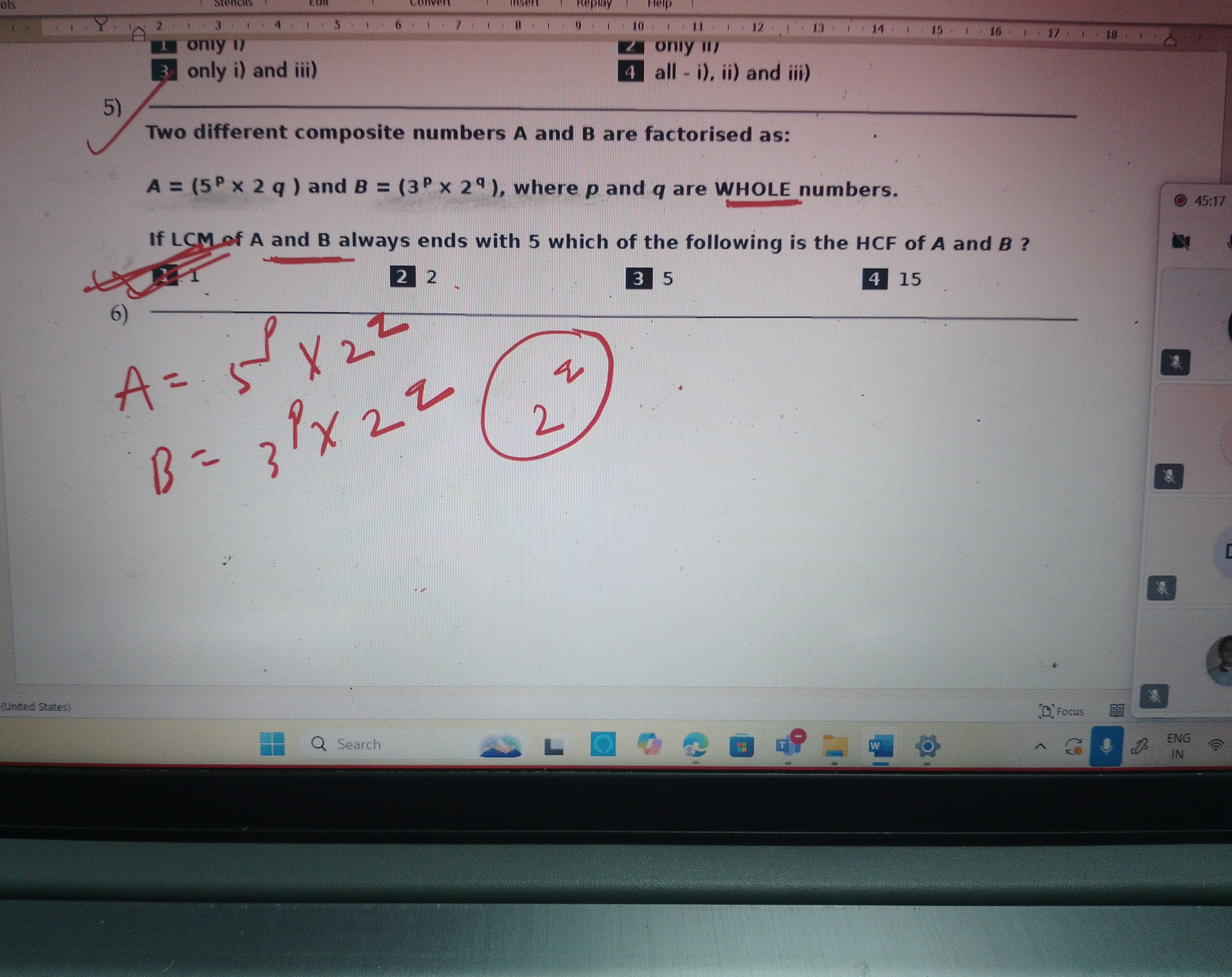
• A. 2
• B. 5
• C. 15
• D. 1

Answer 1

Answer: (D)

1

Answer 2

To ensure that the LCM of A and B ends with 5 (i.e., is odd), there must be no factor of 2. This forces q = 0. Hence,

$A = 5^p$ and $B = 3^p$.

Since 5 and 3 are distinct primes, their only common factor is 1. Thus,

HCF = 1.