Solveeit Logo
Login

Question

Question: The value of $\frac{(1^4 + \frac{1}{4})(3^4 + \frac{1}{4})....(2n-1)^4 + \frac{1}{4})}{(2^4 + \frac{...

The value of (14+14)(34+14)....(2n−1)4+14)(24+14)(44+14)...(2n)4+14)\frac{(1^4 + \frac{1}{4})(3^4 + \frac{1}{4})....(2n-1)^4 + \frac{1}{4})}{(2^4 + \frac{1}{4})(4^4 + \frac{1}{4})...(2n)^4 + \frac{1}{4})} is equal to:

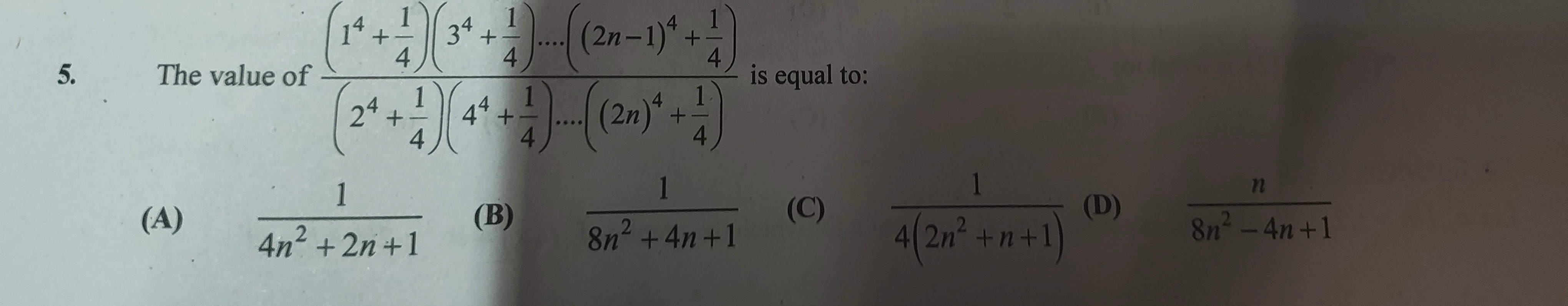
A

14n2+2n+1\frac{1}{4n^2 + 2n + 1}

B

18n2+4n+1\frac{1}{8n^2 + 4n + 1}

C

14(2n2+n+1)\frac{1}{4(2n^2 + n + 1)}

D

n8n2−4n+1\frac{n}{8n^2 - 4n + 1}

Answer

(B) 18n2+4n+1\frac{1}{8n^2+4n+1}

Explanation

Solution

Solution:

We note that for any real number xx

x4+14=(x2+x+12)(x2−x+12).x^4+\frac{1}{4}=\Bigl(x^2+x+\frac{1}{2}\Bigr)\Bigl(x^2-x+\frac{1}{2}\Bigr).

For the numerator when x=2k−1x=2k-1:

(2k−1)4+14=[(2k−1)2+(2k−1)+12][(2k−1)2−(2k−1)+12].(2k-1)^4+\frac{1}{4}=\Bigl[(2k-1)^2+(2k-1)+\frac{1}{2}\Bigr]\Bigl[(2k-1)^2-(2k-1)+\frac{1}{2}\Bigr].

Compute

(2k−1)2=4k2−4k+1.(2k-1)^2=4k^2-4k+1.

Then,

(2k−1)2+(2k−1)+12=4k2−4k+1+2k−1+12=4k2−2k+12,(2k-1)^2+(2k-1)+\frac{1}{2}=4k^2-4k+1+2k-1+\frac{1}{2}=4k^2-2k+\frac{1}{2},

and

(2k−1)2−(2k−1)+12=4k2−4k+1−2k+1+12=4k2−6k+52.(2k-1)^2-(2k-1)+\frac{1}{2}=4k^2-4k+1-2k+1+\frac{1}{2}=4k^2-6k+\frac{5}{2}.

Similarly, for the denominator with x=2kx=2k:

(2k)4+14=[(2k)2+2k+12][(2k)2−2k+12],(2k)^4+\frac{1}{4}=\Bigl[(2k)^2+2k+\frac{1}{2}\Bigr]\Bigl[(2k)^2-2k+\frac{1}{2}\Bigr],

where

(2k)2=4k2,(2k)^2=4k^2,

so that

(2k)2+2k+12=4k2+2k+12,(2k)2−2k+12=4k2−2k+12.(2k)^2+2k+\frac{1}{2}=4k^2+2k+\frac{1}{2},\quad (2k)^2-2k+\frac{1}{2}=4k^2-2k+\frac{1}{2}.

Thus, the kthk^{\text{th}} term in the product becomes:

T(k)=(4k2−2k+12)(4k2−6k+52)(4k2+2k+12)(4k2−2k+12)=4k2−6k+524k2+2k+12.T(k)=\frac{(4k^2-2k+\frac{1}{2})(4k^2-6k+\frac{5}{2})}{(4k^2+2k+\frac{1}{2})(4k^2-2k+\frac{1}{2})}=\frac{4k^2-6k+\frac{5}{2}}{4k^2+2k+\frac{1}{2}}.

Multiplying numerator and denominator by 2 to clear fractions:

T(k)=8k2−12k+58k2+4k+1.T(k)=\frac{8k^2-12k+5}{8k^2+4k+1}.

Notice that

8k2−12k+5=8(k−1)2+4(k−1)+1.8k^2-12k+5=8(k-1)^2+4(k-1)+1.

Thus,

T(k)=8(k−1)2+4(k−1)+18k2+4k+1.T(k)=\frac{8(k-1)^2+4(k-1)+1}{8k^2+4k+1}.

The full product from k=1k=1 to nn telescopes:

P=∏k=1nT(k)=8(0)2+4(0)+18n2+4n+1=18n2+4n+1.P=\prod_{k=1}^{n}T(k)=\frac{8(0)^2+4(0)+1}{8n^2+4n+1}=\frac{1}{8n^2+4n+1}.

Hence, the correct answer is Option (B).

Explanation (Brief):

Factorize x4+14x^4+\tfrac{1}{4} as (x2+x+12)(x2−x+12)(x^2+x+\tfrac{1}{2})(x^2-x+\tfrac{1}{2}). Write the kthk^{\text{th}} term for odd and even arguments, simplify to obtain

T(k)=8k2−12k+58k2+4k+1=8(k−1)2+4(k−1)+18k2+4k+1.T(k)=\frac{8k^2-12k+5}{8k^2+4k+1}=\frac{8(k-1)^2+4(k-1)+1}{8k^2+4k+1}.

The telescoping product yields

18n2+4n+1.\frac{1}{8n^2+4n+1}.