Question

The length of the focal chord of the ellipse $\frac{x^2}{16} + \frac{y^2}{9} = 1$ which is inclined to the major axis at angle $\frac{\pi}{3}$ is A then the value of [A] (Where [] denotes greatest integer function) is equal to

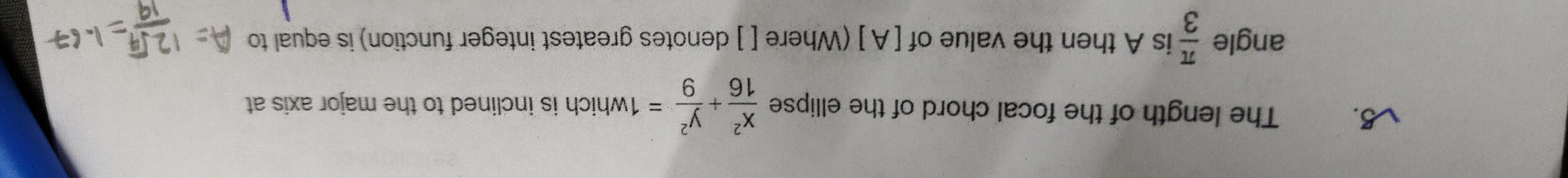
• A. 2
• B. 15
• C. 12
• D. 3

Answer 1

Answer: (A)

2

Answer 2

The length of a focal chord of an ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ inclined at an angle $\theta$ to the major axis is given by $L = \frac{ab^2}{a^2 \sin^2 \theta + b^2 \cos^2 \theta}$. For the given ellipse, $a=4$, $b=3$ and $\theta = \frac{\pi}{3}$. Substituting these values, we get $L = \frac{4 \cdot 3^2}{4^2 \cdot (\frac{\sqrt{3}}{2})^2 + 3^2 \cdot (\frac{1}{2})^2} = \frac{36}{16 \cdot \frac{3}{4} + 9 \cdot \frac{1}{4}} = \frac{36}{12 + \frac{9}{4}} = \frac{36}{\frac{57}{4}} = \frac{144}{57} = \frac{48}{19}$. The length $A = \frac{48}{19}$. The greatest integer $[A] = [\frac{48}{19}] = [2.526...] = 2$.