Question

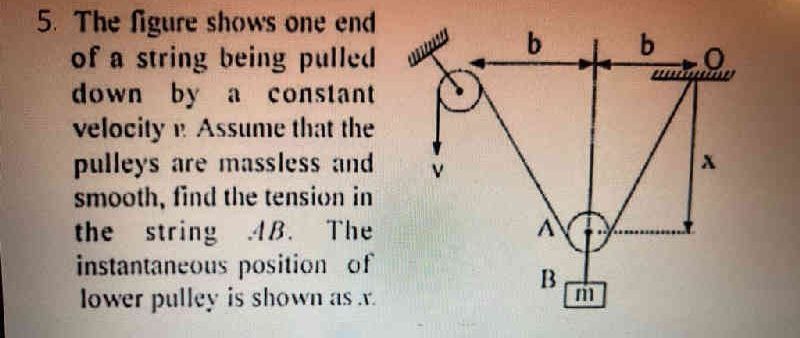
The figure shows one end of a string being pulled down by a constant velocity $v$. Assume that the pulleys are massless and smooth, find the tension in the string $AB$. The instantaneous position of lower pulley is shown as $x$.

Answer 1

Tension in the string AB is $T_{AB} = mg$.

Answer 2

We shall show that, even though one end of the “support‐rope” is pulled down at a constant speed, the mass m (attached by the string AB) is lifted at constant speed and, after using the geometrical (inextensibility) constraint and force–balance on the movable pulley, one finds that the tension in the string AB is simply

$$T_{AB}=mg.$$

Solution:

1. The Setup:
   A mass m (point B) is attached to a movable pulley (point A) by a string AB. The movable pulley A is supported by a rope that has one end being pulled downward at a constant speed v and that goes over smooth pulleys. (The geometry gives an inclined segment from A to a fixed pulley at O; the angle θ is given by $\cos\theta=\dfrac{\text{vertical separation}}{\sqrt{x^2+b^2}}$; see diagram.)

2. Kinematic Constraint:
   Since the rope is inextensible, if the free end is pulled down with speed v, and the portion coming vertically from one side shortens by the upward speed u of A while the other (inclined) segment shortens by $u\cos\theta$, then

   $$v=u+u\cos\theta \quad \Longrightarrow \quad u=\frac{v}{1+\cos\theta}\,.$$

3. Force Balance on the Movable Pulley A:
   The movable pulley is massless so the net force on it must vanish. It is supported by two segments of the support rope that, because the pulleys are smooth, have the same tension (say $T_0$). One segment is vertical (providing an upward force $T_0$) and the other, being inclined, contributes an upward component $T_0\cos\theta$. Thus the net upward force on A is

   $$T_0(1+\cos\theta).$$

   But the pulley supports the load m via the string AB. In our usual ideal pulley system the tension in the string AB (which we call $T_{AB}$) simply “pulls down” on A. Equating forces we have

   $$T_0(1+\cos\theta)=T_{AB}\,.$$

4. Force Balance on the Mass m (B):
   The mass m is moving at constant speed so its net force is zero; hence the upward tension in the string AB must balance its weight:

   $$T_{AB}=mg.$$

5. Conclusion:
   Thus we find that

   $$T_{AB}=mg\,,$$

   which is independent of the pulling speed v and the geometric position (x, b).