Question

The complete set of values the parameter 'a' so that the point $P(a, \frac{1}{1+a^2})$ doesn't lie outside the triangle formed by the lines $15y = x + 1, 78y = 118 - 23x$ and $y + 2 = 0$ is -

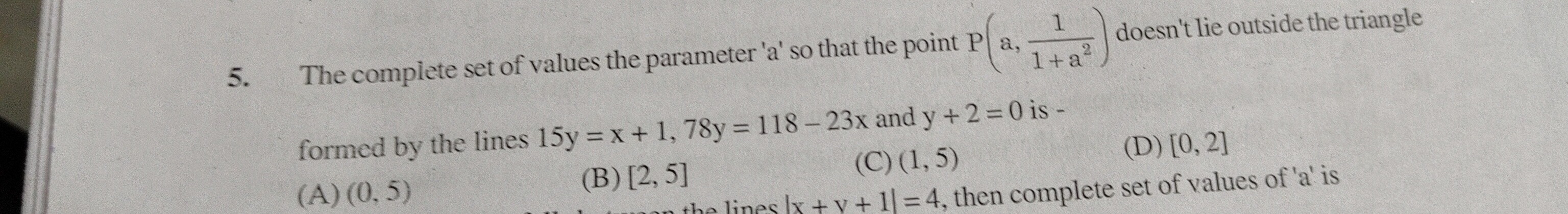
• A. (0, 5)
• B. [2, 5]
• C. (1, 5)
• D. [0, 2]

Answer 1

Answer: (B)

[2, 5]

Answer 2

The problem asks for the complete set of values of the parameter 'a' such that the point $P(a, \frac{1}{1+a^2})$ lies inside or on the boundary of the triangle formed by three given lines.

Let the three lines be:

1. $L_1: x - 15y + 1 = 0$
2. $L_2: 23x + 78y - 118 = 0$
3. $L_3: y + 2 = 0$

To determine the region of the triangle, we first find its vertices:

• Vertex A (Intersection of $L_1$ and $L_3$): Substitute $y = -2$ into $L_1$: $x - 15(-2) + 1 = 0 \Rightarrow x + 30 + 1 = 0 \Rightarrow x = -31$. So, $A = (-31, -2)$.
• Vertex B (Intersection of $L_2$ and $L_3$): Substitute $y = -2$ into $L_2$: $23x + 78(-2) - 118 = 0 \Rightarrow 23x - 156 - 118 = 0 \Rightarrow 23x = 274 \Rightarrow x = \frac{274}{23}$. So, $B = (\frac{274}{23}, -2)$.
• Vertex C (Intersection of $L_1$ and $L_2$): From $L_1$, $x = 15y - 1$. Substitute into $L_2$: $23(15y - 1) + 78y - 118 = 0$ $345y - 23 + 78y - 118 = 0$ $423y - 141 = 0 \Rightarrow y = \frac{141}{423} = \frac{1}{3}$. Substitute $y = \frac{1}{3}$ back into $x = 15y - 1$: $x = 15(\frac{1}{3}) - 1 = 5 - 1 = 4$. So, $C = (4, \frac{1}{3})$.

The vertices of the triangle are $A(-31, -2)$, $B(\frac{274}{23}, -2)$, and $C(4, \frac{1}{3})$.

For a point $P(x_P, y_P)$ to lie inside or on the boundary of the triangle, it must satisfy the conditions that it lies on the same side of each line as the third vertex. Let's determine the correct inequalities for the region:

• For $L_1: x - 15y + 1 = 0$: Check vertex $B(\frac{274}{23}, -2)$ (not on $L_1$). $L_1(B) = \frac{274}{23} - 15(-2) + 1 = \frac{274}{23} + 30 + 1 = \frac{274}{23} + 31 = \frac{274 + 713}{23} = \frac{987}{23} > 0$. So, the region is $x - 15y + 1 \ge 0$.
• For $L_2: 23x + 78y - 118 = 0$: Check vertex $A(-31, -2)$ (not on $L_2$). $L_2(A) = 23(-31) + 78(-2) - 118 = -713 - 156 - 118 = -987 < 0$. So, the region is $23x + 78y - 118 \le 0$.
• For $L_3: y + 2 = 0$: Check vertex $C(4, \frac{1}{3})$ (not on $L_3$). $L_3(C) = \frac{1}{3} + 2 = \frac{7}{3} > 0$. So, the region is $y + 2 \ge 0$.

Now, substitute the coordinates of point $P(a, \frac{1}{1+a^2})$ into these inequalities:

Condition 1: $a - 15(\frac{1}{1+a^2}) + 1 \ge 0$ Multiply by $(1+a^2)$ (which is always positive since $a^2 \ge 0$): $a(1+a^2) - 15 + (1+a^2) \ge 0$ $a + a^3 - 15 + 1 + a^2 \ge 0$ $a^3 + a^2 + a - 14 \ge 0$ Let $f(a) = a^3 + a^2 + a - 14$. By inspection, $f(2) = 2^3 + 2^2 + 2 - 14 = 8 + 4 + 2 - 14 = 0$. So $(a-2)$ is a factor. Dividing $f(a)$ by $(a-2)$ gives $a^2 + 3a + 7$. $f(a) = (a-2)(a^2 + 3a + 7)$. The quadratic factor $a^2 + 3a + 7$ has discriminant $\Delta = 3^2 - 4(1)(7) = 9 - 28 = -19 < 0$. Since the leading coefficient is positive, $a^2 + 3a + 7$ is always positive for all real $a$. Therefore, for $f(a) \ge 0$, we must have $a-2 \ge 0$, which implies $a \ge 2$.

Condition 2: $23a + 78(\frac{1}{1+a^2}) - 118 \le 0$ Multiply by $(1+a^2)$: $23a(1+a^2) + 78 - 118(1+a^2) \le 0$ $23a + 23a^3 + 78 - 118 - 118a^2 \le 0$ $23a^3 - 118a^2 + 23a - 40 \le 0$ Let $g(a) = 23a^3 - 118a^2 + 23a - 40$. By inspection, $g(5) = 23(5^3) - 118(5^2) + 23(5) - 40 = 23(125) - 118(25) + 115 - 40 = 2875 - 2950 + 115 - 40 = 0$. So $(a-5)$ is a factor. Dividing $g(a)$ by $(a-5)$ gives $23a^2 - 3a + 8$. $g(a) = (a-5)(23a^2 - 3a + 8)$. The quadratic factor $23a^2 - 3a + 8$ has discriminant $\Delta = (-3)^2 - 4(23)(8) = 9 - 736 = -727 < 0$. Since the leading coefficient is positive, $23a^2 - 3a + 8$ is always positive for all real $a$. Therefore, for $g(a) \le 0$, we must have $a-5 \le 0$, which implies $a \le 5$.

Condition 3: $\frac{1}{1+a^2} + 2 \ge 0$ Since $a^2 \ge 0$, $1+a^2 \ge 1$. This means $0 < \frac{1}{1+a^2} \le 1$. Thus, $\frac{1}{1+a^2} + 2$ will always be greater than $2$ (specifically, $2 < \frac{1}{1+a^2} + 2 \le 3$). So, this condition is always satisfied for all real $a$.

Combining the conditions $a \ge 2$ and $a \le 5$, we get the interval $[2, 5]$. This means that for any $a$ in the interval $[2, 5]$, the point $P(a, \frac{1}{1+a^2})$ will lie inside or on the boundary of the given triangle.