Question

Tangents are drawn from the point (-1,2) on the parabola $y^2=4x$. Find the length, these tangents will intercept on the line x=2.

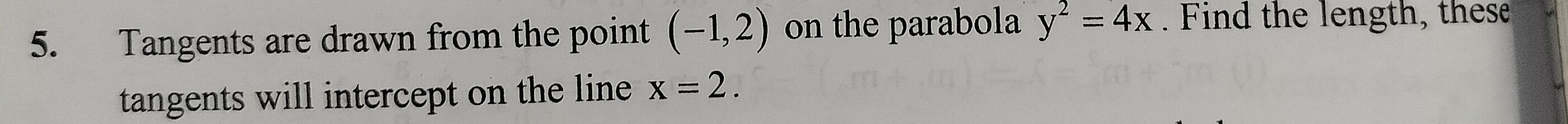
Answer 1

The length of the intercept is $6\sqrt{2}$.

Answer 2

1. The equation of the parabola is $y^2 = 4x$, which implies $a=1$.
2. The general equation of a tangent to the parabola $y^2=4ax$ is $y = mx + \frac{a}{m}$. For $a=1$, this becomes $y = mx + \frac{1}{m}$.
3. Since the tangents are drawn from the point $(-1, 2)$, substituting these coordinates into the tangent equation gives $2 = m(-1) + \frac{1}{m}$.
4. Multiplying by $m$ and rearranging yields the quadratic equation for the slopes of the tangents: $m^2 + 2m - 1 = 0$. Let the roots be $m_1$ and $m_2$.
5. From Vieta's formulas, $m_1 + m_2 = -2$ and $m_1 m_2 = -1$.
6. The line on which the intercept is to be found is $x=2$. The y-coordinates of the points where the tangents intersect the line $x=2$ are $y_1 = 2m_1 + \frac{1}{m_1}$ and $y_2 = 2m_2 + \frac{1}{m_2}$.
7. The length of the intercept, $L$, is the absolute difference between these y-coordinates: $L = |y_1 - y_2| = |(2m_1 + \frac{1}{m_1}) - (2m_2 + \frac{1}{m_2})|$.
8. This simplifies to $L = |2(m_1 - m_2) + (\frac{1}{m_1} - \frac{1}{m_2})| = |2(m_1 - m_2) + \frac{m_2 - m_1}{m_1 m_2}| = |(m_1 - m_2)(2 - \frac{1}{m_1 m_2})|$.
9. Substituting $m_1 m_2 = -1$, we get $L = |(m_1 - m_2)(2 - \frac{1}{-1})| = |3(m_1 - m_2)|$.
10. To find $|m_1 - m_2|$, we use the identity $(m_1 - m_2)^2 = (m_1 + m_2)^2 - 4m_1 m_2$. Substituting the values: $(m_1 - m_2)^2 = (-2)^2 - 4(-1) = 4 + 4 = 8$. Thus, $|m_1 - m_2| = \sqrt{8} = 2\sqrt{2}$.
11. Finally, $L = 3 \times |m_1 - m_2| = 3 \times 2\sqrt{2} = 6\sqrt{2}$.