Question

Suppose that the function $f(x) = \log_c \frac{x-2}{x+2}$ is defined for all x in the interval [a, b], is monotonic decreasing. Find the value of 'c' for which there exists 'a' and 'b' (b>a>2) such that the range of the function is $[\log_c(b-1), \log_c(a-1)]$.

Answer 1

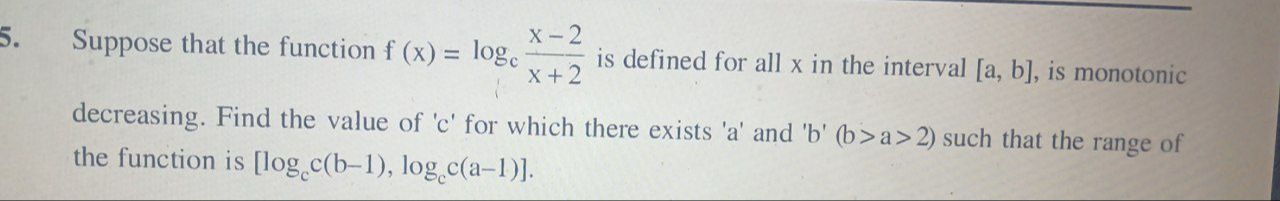
No such value of 'c' exists.

Answer 2

The function $f(x) = \log_c \frac{x-2}{x+2}$ is defined for $x \in (-\infty, -2) \cup (2, \infty)$. Let $g(x) = \frac{x-2}{x+2} = 1 - \frac{4}{x+2}$. For $x > 2$, $g(x)$ is monotonically increasing. For $f(x) = \log_c(g(x))$ to be monotonically decreasing, the base $c$ must satisfy $0 < c < 1$.

The range of $f(x)$ on $[a, b]$ is given as $[\log_c(b-1), \log_c(a-1)]$. Since $f(x)$ is decreasing and $b > a$, the range should be $[f(b), f(a)]$. Thus, $f(a) = \log_c(a-1)$ and $f(b) = \log_c(b-1)$.

Substituting the function definition: $\log_c\left(\frac{a-2}{a+2}\right) = \log_c(a-1) \implies \frac{a-2}{a+2} = a-1$ $\log_c\left(\frac{b-2}{b+2}\right) = \log_c(b-1) \implies \frac{b-2}{b+2} = b-1$

Solving $\frac{x-2}{x+2} = x-1$: $x-2 = (x-1)(x+2) = x^2 + x - 2$ $x^2 = 0 \implies x = 0$.

This implies $a=0$ and $b=0$. However, the problem states $b > a > 2$. This is a contradiction. Therefore, no such values of $a$ and $b$ exist for any $c$.