Solveeit Logo
Login

Question

Question: P is a point on the parabola $y^2 = 4x$ and Q is a point on the line $2x + y + 4 = 0$. If the line $...

P is a point on the parabola y2=4xy^2 = 4x and Q is a point on the line 2x+y+4=02x + y + 4 = 0. If the line x−y+1=0x-y+ 1 = 0 is the perpendicular bisector of PQ, then the co-ordinates of P can be :

A

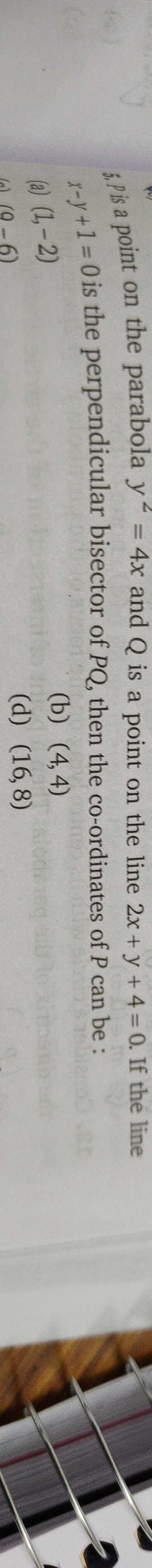
(1,-2)

B

(4,4)

C

(9,-6)

D

(16,8)

Answer

(1,-2) and (9,-6)

Explanation

Solution

Let P(t2,2t)(t^2, 2t) be a point on the parabola y2=4xy^2=4x. The line x−y+1=0x-y+1=0 is the perpendicular bisector of PQ. This means:

  1. The midpoint of PQ lies on x−y+1=0x-y+1=0.
  2. The slope of PQ is −1-1 (perpendicular to the slope of x−y+1=0x-y+1=0, which is 1).

From condition 2, if Q is (xQ,yQ)(x_Q, y_Q), then yQ−2txQ−t2=−1\frac{y_Q - 2t}{x_Q - t^2} = -1. yQ−2t=−(xQ−t2)y_Q - 2t = -(x_Q - t^2) yQ−2t=−xQ+t2y_Q - 2t = -x_Q + t^2 xQ+yQ=t2+2tx_Q + y_Q = t^2 + 2t.

Since Q lies on 2x+y+4=02x+y+4=0, we have 2xQ+yQ=−42x_Q + y_Q = -4. Subtracting the two equations: (2xQ+yQ)−(xQ+yQ)=−4−(t2+2t)(2x_Q + y_Q) - (x_Q + y_Q) = -4 - (t^2 + 2t) xQ=−t2−2t−4x_Q = -t^2 - 2t - 4.

Substitute xQx_Q into xQ+yQ=t2+2tx_Q + y_Q = t^2 + 2t: (−t2−2t−4)+yQ=t2+2t(-t^2 - 2t - 4) + y_Q = t^2 + 2t yQ=2t2+4t+4y_Q = 2t^2 + 4t + 4.

Now, the midpoint of PQ, M=(t2+xQ2,2t+yQ2)M = \left(\frac{t^2+x_Q}{2}, \frac{2t+y_Q}{2}\right), lies on x−y+1=0x-y+1=0. M=(t2+(−t2−2t−4)2,2t+(2t2+4t+4)2)M = \left(\frac{t^2 + (-t^2 - 2t - 4)}{2}, \frac{2t + (2t^2 + 4t + 4)}{2}\right) M=(−2t−42,2t2+6t+42)M = \left(\frac{-2t-4}{2}, \frac{2t^2+6t+4}{2}\right) M=(−t−2,t2+3t+2)M = (-t-2, t^2+3t+2).

Substitute M into x−y+1=0x-y+1=0: (−t−2)−(t2+3t+2)+1=0(-t-2) - (t^2+3t+2) + 1 = 0 −t−2−t2−3t−2+1=0-t-2 - t^2-3t-2 + 1 = 0 −t2−4t−3=0-t^2 - 4t - 3 = 0 t2+4t+3=0t^2 + 4t + 3 = 0 (t+1)(t+3)=0(t+1)(t+3) = 0. So, t=−1t=-1 or t=−3t=-3.

If t=−1t=-1, P is ((−1)2,2(−1))=(1,−2)((-1)^2, 2(-1)) = (1, -2). If t=−3t=-3, P is ((−3)2,2(−3))=(9,−6)((-3)^2, 2(-3)) = (9, -6).