Question

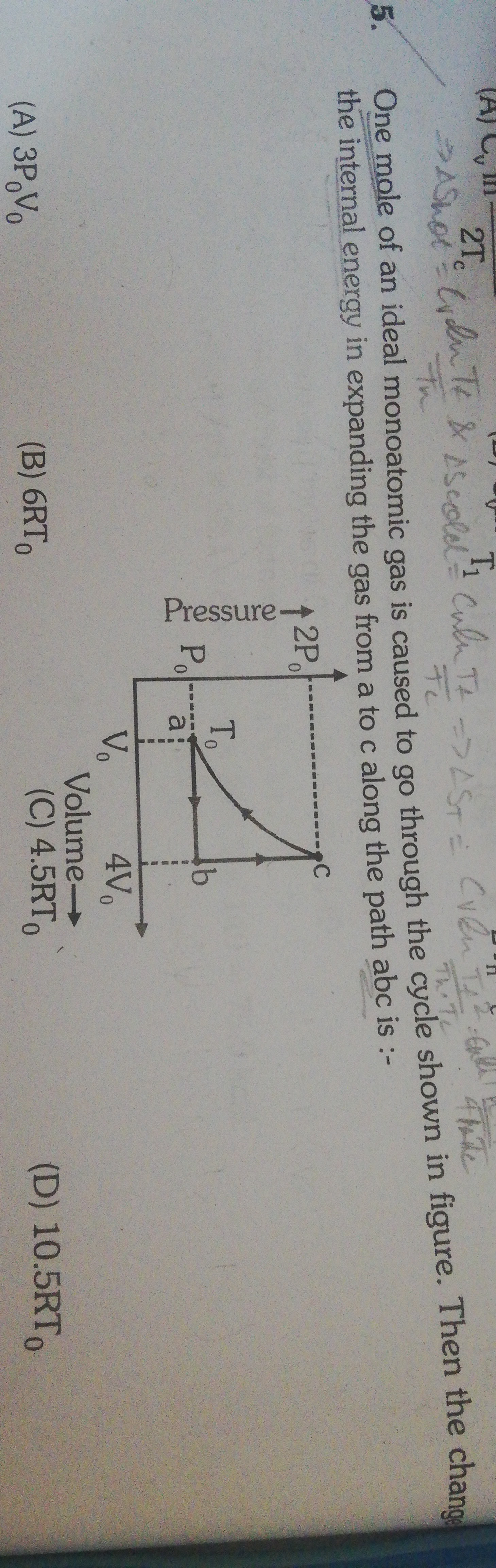
One mole of an ideal monoatomic gas is caused to go through the cycle shown in figure. Then the change the internal energy in expanding the gas from a to c along the path abc is :-

• A. 3P₀V₀
• B. 6RT₀
• C. 4.5RT₀
• D. 10.5RT₀

Answer 1

Answer: (D)

10.5RT₀

Answer 2

The internal energy of an ideal gas depends only on its temperature. For one mole of a monoatomic ideal gas, the internal energy is given by $U = \frac{3}{2}RT$. The change in internal energy is $\Delta U = \frac{3}{2}R(T_f - T_i)$.

From the P-V diagram, state 'a' has pressure $P_0$ and volume $V_0$. Assuming $n=1$ mole, $P_0V_0 = RT_a$. Let $T_a = T_0$. So, $P_0V_0 = RT_0$.

State 'c' has pressure $2P_0$ and volume $4V_0$. The temperature at state 'c' is $T_c = \frac{P_c V_c}{R} = \frac{(2P_0)(4V_0)}{R} = \frac{8P_0V_0}{R}$. Substituting $P_0V_0 = RT_0$, we get $T_c = \frac{8RT_0}{R} = 8T_0$.

The change in internal energy from 'a' to 'c' is $\Delta U = \frac{3}{2}R(T_c - T_a) = \frac{3}{2}R(8T_0 - T_0) = \frac{3}{2}R(7T_0) = 10.5 RT_0$. The path taken ('abc') does not affect the change in internal energy, as it is a state function.